0x00-基础算法-(5)-前缀和&差分

前缀和

前缀和主要起优化作用，只要花费 $O(n)$ 的预处理，它可以在 $O(1)$ 内求出原数组某段的子数组和。

当你要多次求原数组中某一段子数组和，就可以考虑用前缀和优化

一维前缀和

定义

原数组: $\{a_1 , a_2, a_3, ... ,a_n \}$

前缀和数组: $\{S_1 , S_2, S_3, ... ,S_n \}$ ，其中 $S_i = a_1 + a_2 + ... + a_i$ ，规定边界 $S_0 = 0$

代码实现(1-based)

存储时for循环最好要让下标从1开始，让 $S_0 = 0$ ，这样就不用处理边界问题

#include <vector>
#include <iostream>

using namespace std;

const int N = 1e6 + 10;
vector<int> arr(N);
vector<int> sum(N);

int main() {
    int n, m;
	cin >> n >> m;
   
    for (int i = 1; i <= n; i ++) scanf("%d", &arr[i]);
    
    // 预处理前缀和
    for (int i = 1; i <= n; i ++) sum[i] = sum[i - 1] + arr[i];
    
    // m次询问区间[l, r]
    while (m --) {
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%d\n", sum[r] - sum[l - 1]);
    }
}

时间复杂度分析

以一维前缀和为例，当你要多次(假设m次)求原数组(长度为n)中某一段子数组和的时候:

如果没有前缀和，每求一段需要循环遍历一次数组, 1次时间复杂度 $O(n)$ , m次时间复杂度 $O(mn)$ ;
当你存储了前缀和(预处理花费时间复杂度 $O(n)$ , 求其中某一段 $[l,r]$ 的子数组和, 只要用 $S_r-S_{l-1}$ 即可, 1次时间复杂度 $O(1)$ ，m次时间复杂度 $O(m)$ ，共 $O(m+n)$ .

二维前缀和

定义

原二维数组( $n \times m$ ):

$\begin{bmatrix} a_{11} &a_{12} &... &a_{1m}\\ a_{21} &a_{22} &... &a_{2m} \\ ... &... &... &... \\ a_{n1} &a_{n2} &... &a_{nm} \end{bmatrix}$

二维前缀和数组( $n \times m$ ):

$\begin{bmatrix} S_{11} &S_{12} &... &S_{1m}\\ S_{21} &S_{22} &... &S_{2m} \\ ... &... &... &... \\ S_{n1} &S_{n2} &... &S_{nm} \end{bmatrix}$

其中 $S_{ij} = \begin{bmatrix} a_{11} &... &a_{1j}\\ ... &... &... \\ a_{i1} &... &a_{ij} \end{bmatrix}$ , 规定边界 $S_0 = 0$

代码实现(1-based)

#include <vector>
#include <iostream>

using namespace std;

const int N = 1e3 + 10;

vector<vector<int>> arr(N, vector<int>(N));
vector<vector<int>> sum(N, vector<int>(N));

int main() {
	int n, m, q;
	cin >> n >> m >> q;
	
	for (int i = 1; i <= n; i ++) {
		for (int j = 1; j <= m; j ++) {
			scanf("%d", &arr[i][j]);
		}
	}
	
    // 预处理二维前缀和
	for (int i = 1; i <= n; i ++) {
		for (int j = 1; j <= m; j ++) {
			sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1] + arr[i][j];
		}
	}
	
    // m次询问[(x1, y1),(x2, y2)]
	while (q --) {
		int x1, y1, x2, y2;
		scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
		int ans = sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];
		printf("%d\n", ans);
	}

	return 0;
}

二维前缀和有两种询问方式：

目标子矩阵之和：已知左上角 $(x1, y1)$ ，右下角坐标 $(x2, y2)$

// 区间[(x1, y1), (x2, y2)]
int tar = sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];

目标子矩阵之和：已知宽 $w$ ，高 $h$ ，右下角坐标 $(x, y)$

// 区间[(x - h + 1, y - w + 1), (x, y)]
int tar = sum[x][y] - sum[x - h][y] - sum[x][y - w] + sum[x - h][y - w];

时间复杂度分析

待续

练习eg:

Acwing-121.赶牛入圈

Acwing-126.最大的和

PS:
为了节省空间，可以原地处理（只要题目不需要同时使用前缀和）：
一维：
for (int i = 1; i <= n; i ++) {
	scanf("%d", &arr[i]);
	arr[i] += arr[i - 1];
}
二维：
for (int i = 1; i <= n; i ++) {
    for (int j = 1; j <= m; j ++) {
        scanf("%d", &arr[i][j]);
        arr[i][j] += arr[i - 1][j] + arr[i][j - 1] - arr[i - 1][j - 1];
    }
}
用完前缀和之后可以再对前缀和数组差分，还原回原数组

差分

差分主要起优化作用，只要花费 $O(n)$ 的预处理，它可以在 $O(1)$ 内给原数组中的某一段 ${[l,r]}$ 子数组区间加上一个固定的常数 ${C}$ 。

一维差分

定义

${b_{i} = a_{i} - a_{i-1}}$ , 规定 ${b_1 = a_1}$

一维差分数组与原数组的转换(1-based)

构造差分数组时，可以看作是在所有初始值为0的一段区间中，在 ${[i, i]}$ 区间插入了 ${arr[i]}$ 。

时间复杂度分析

同理于一维前缀和，预处理需要花费 $O(n)$ ，此后单次 ${insert}$ 操作时间复杂度 $O(1)$ ， ${m}$ 次时间复杂度 $O(m)$ ，总共 $O(m + n)$

练习eg:

Acwing-100.增减序列

二维差分

定义

二维差分数组与原数组的转换(1-based)

原数组=>二维差分数组

同理于一维，构造差分数组时，可以看作是在所有初始值为0的一片区间中，在 ${[(i, j), (i,j)]}$ 点插入了 ${arr[i][j]}$ 。

int a[N][N];   // 原数组
int d[N][N];   // 二维差分数组

// 在以左上角(x1, y1), 右下角(x2, y2)包围的子矩阵[包含边界]中插入数值c
inline void insert(int x1, int y1, int x2, int y2, int c) {
    d[x1][y1] += c;
    d[x2 + 1][y1] -= c;
    d[x1][y2 + 1] -= c;
    d[x2 + 1][y2 + 1] += c;
}

int main() {
    cin >> n;
    // 1-based
    for (int i = 1; i <= n; ++ i) {
        for (int j = 1; j <= n; ++ j) {
            cin >> a[i][j];
            insert(i, j, i, j, a[i][j]);
        }
    }
}

二维差分数组=>原数组

int a[N][N];   // 原数组
int d[N][N];   // 二维差分数组

int main() {
    for (int i = 1; i <= n; ++ i) {
        for (int j = 1; j <= n; ++ j) {
            // a[i][j] = d[i][j] + d[i - 1][j] + d[i][j - 1] - d[i - 1][j - 1];
            // 通常直接在原地还原，节省空间
            d[i][j] += d[i - 1][j] + d[i][j - 1] - d[i - 1][j - 1];
        }
    }
}

时间复杂度分析

0-based

LeetCode上的前缀和&后缀和

做法：统一把前缀和和后缀和，往后偏移1位，用下标[1-n]的位置存储

这样做的好处，就是不用特殊判断数组越界。

// 一般传入参数会给一个 vector<int> arr; 那么应该怎么求前/后缀和呢？

class Solution {
public:
    vector<int> preAndsuf(int arr) {
        int n = arr.size();
        
        // 前缀和pre
        vector<int> pre(n + 2); //pre(n + 1);也可以，统一n + 2
        // 后缀和suf
        vector<int> suf(n + 2);
        // pre
        for (int i = 1, c = 0; i <= n; i ++) {
			pre[i] = pre[i - 1] + arr[i - 1];
        }
        // suf
        for (int i = n, c = 0; i >= 1; i --) {
            suf[i] = suf[i + 1] + arr[i - 1];
        }

        // 使用1: 利用前缀和/后缀和，求arr中区间[l, r]的区间和
        int l = 0, r = n - 1;
        int sum_lr = pre[r + 1] - pre[(l + 1) - 1]; // 利用前缀和求
        int sum_lr = suf[l + 1] - suf[(r + 1) + 1]; // 利用后缀和求
        // 使用2: 求对应位置的前后缀和之和
        vector<int> res;
        for (int i = 1; i <= n; i ++) {
            res.emplace_back(pre[i] + suf[i]);
        }

        return res;
    }
};

LeetCode上的差分数组

LeetCode-2536.子矩阵元素+1

class Solution {
public:
    vector<vector<int>> rangeAddQueries(int n, vector<vector<int>>& queries) {
        // 差分矩阵
        vector<vector<int>> b(n + 2, vector<int> (n + 2, 0));
        
        for (auto q : queries) {
            // 要整体偏移1个单位下标
            int x1 = q[0] + 1, y1 = q[1] + 1;
            int x2 = q[2] + 1, y2 = q[3] + 1;
            
            b[x1][y1] += 1;
            b[x2 + 1][y1] -= 1;
            b[x1][y2 + 1] -= 1;
            b[x2 + 1][y2 + 1] += 1;
        }
        
        for (int i = 1; i <= n; i ++) {
            for (int j = 1; j <= n; j ++) {
                b[i][j] = b[i][j] + b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
            }
        }     
        
        vector<vector<int>> res(n, vector<int> (n, 0));
        for (int i = 0; i < n; i ++) {
            for (int j = 0; j < n; j ++) {
                res[i][j] = b[i + 1][j + 1];
            }
        }
        
        return res;
    }
};

总结一下

leetcode上的题目通常会给vector，因此是0-base的(下标从0开始)

一般比较好写的是1-base的，你就需要在使用前，偏移一个单位处理.

开(n + 2)大小的数组，转换成1-based的写

应用

LeetCode-1895.最大的幻方

行列前缀和暴力，典中典的题目

求行的和，列的和，对角线的和，非常基础非常好:

class Solution {
public:
    int largestMagicSquare(vector<vector<int>>& grid) {
        int n = grid.size();
        int m = grid[0].size();

        vector<vector<int>> rowsum(n + 1, vector<int> (m + 1));
        vector<vector<int>> colsum(n + 1, vector<int> (m + 1));
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= m; ++j) {
                rowsum[i][j] = rowsum[i][j - 1] + grid[i - 1][j - 1];
                colsum[i][j] = colsum[i - 1][j] + grid[i - 1][j - 1];
            }
        }
        

        auto check = [&](int x1, int y1, int x2, int y2) -> bool {
            // 求[l ,r] => s[r] - s[l - 1]，但这里用的下标是原数组grid的，因此是s[r + 1] - s[l]
            unordered_set<int> st;
            // 行
            for (int i = x1; i <= x2; ++i) {
                st.insert(rowsum[i + 1][y2 + 1] - rowsum[i + 1][y1]);
                if (st.size() > 1) return false;
            }
            // 列
            for (int j = y1; j <= y2; ++j) {
                st.insert(colsum[x2 + 1][j + 1] - colsum[x1][j + 1]);
                if (st.size() > 1) return false;
            }
            // 对角线
            int s = 0;
            for (int i = x1, j = y1; i <= x2 && j <= y2; ++i, ++j) {
                s += grid[i][j];
            }
            st.insert(s);
            if (st.size() > 1) return false;
            s = 0;
            for (int i = x1, j = y2; i <= x2 && j >= y1; ++i, --j) {
                s += grid[i][j];
            }
            st.insert(s);
            if (st.size() > 1) return false;

            return true;
        };

        for (int k = min(n, m); k >= 1; --k) {
            for (int i = 0; i + k - 1 < n; ++i) {
                for (int j = 0; j + k - 1 < m; ++j) {
                    int i2 = i + k - 1;
                    int j2 = j + k - 1;
                    if (check(i, j, i2, j2)) {
                        return k;
                    }
                }
            }
        }
        return 1;
    }
};

前缀和 + 哈希表

找到一个最长子数组，其元素和等于 0

面试题17.05. 字母与数字

找使得数组内其它元素==当前元素的最小操作次数

关键理解下面这张图，就能写出关键的那三行，求idx，l， r

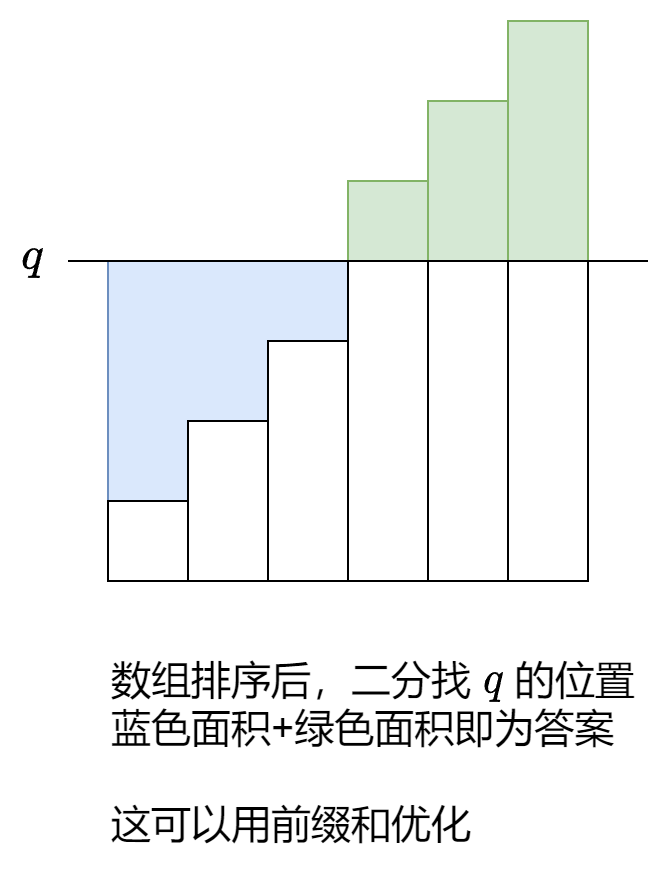
LeetCode-2602.使数组元素全部相等的最少操作次数

class Solution {
public:
    vector<long long> minOperations(vector<int>& nums, vector<int>& queries) {
        int n = nums.size();
        sort(nums.begin(), nums.end());

        // 前缀和
        vector<long long> sum(n + 1);
        for (int i = 1; i <= n; ++ i ) {
            sum[i] = sum[i - 1] + nums[i - 1];
        }
        
        int m = queries.size();
        vector<long long> res(m);
        
        for (int i = 0; i < m; ++ i) {
            int q = queries[i];
            // 二分
            long long j = lower_bound(nums.begin(), nums.end(), q) - nums.begin();
            long long l = j * q - sum[j];
            long long r = (sum[n] - sum[j]) - ((n - j) * q);
            res[i] = l + r;
        }
        return res;   
    }
};

LeetCode-2121.相同元素的间隔之和

class Solution {
typedef long long int64;
public:
    // for (int i = 0; i < n;  ++i) {
    //     int64 cur = 0;
    //     for (int j = 0; j < n; ++j) {
    //         if (arr[i] == arr[j]) {
    //             cur += abs(j - i);
    //         }
    //     }
    //     res.emplace_back(cur);
    // }
    vector<long long> getDistances(vector<int>& arr) {
        int n = arr.size();
        
        unordered_map<int, vector<int>> mp;
        for (int i = 0; i < n; ++i) {
            mp[arr[i]].emplace_back(i);
        }

        vector<int64> res(n, 0);
        for (auto& [_, vec] : mp) {
            int sz = vec.size();
            vector<int64> sum(sz + 1);
            for (int i = 1; i <= sz; ++i) {
                sum[i] = sum[i - 1] + vec[i - 1];
            }

            for (int i = 0; i < sz; ++i) {
                int64 idx = vec[i];
                int64 l = i * idx - sum[i];
                int64 r = (sum[sz] - sum[i]) -  ((sz - i) * idx);
                res[idx] = l + r;
            }
        }

        return res;
    }
};

数据结构与算法

Algorithm Template C++

本博客所有文章均采用 CC BY-NC-SA 4.0 协议，禁止商用，转载请注明出处！

0x00-基础算法-(6)-贪心上一篇

0x00-基础算法-(4)-高精度下一篇