树状数组

树状数组（Binary Index Tree / Fenwick Tree）是一种简单的数据结构，主要用来维护序列的前缀和。
它根据任意正整数关于2的不重复次幂的唯一分解性质，把区间二进制分解，支持在$O(\log n)$对原序列单点更新，同时支持在$O(\log n)$内查询前缀和。

任意正整数关于2的不重复次幂的唯一分解：

就是说：如果我们想查询区间[1, x]，可以先把x进行二进制分解：
假设正整数x的二进制表示为$a_{k - 1}a_{k - 2}\ldots a_2a_1a_0$，其中等于1的位是${\{a_{i_{1}}, a_{i_{2}}, \ldots a_{i_{m}}\}}$，则正整数x可以被二进制分解成：

$x = 2^{i_1} + 2^{i_2} + \ldots + 2^{i_m}$

那么查询区间[1,x]，可以分解成查询以下log(x)个子区间：

• 长度为$2^{i_1}$的子区间$[1, 2^{i_1}]$

• 长度为$2^{i_2}$的子区间$[2^{i_1} + 1, 2^{i_1} + 2^{i_2}]$

• …

• 长度为$2^{i_m}$的子区间$[2^{i_1} + 2^{i_2} + \ldots + 2^{i_{m-1}} + 1, 2^{i_1} + 2^{i_2} + \ldots + 2^{i_m}]$

这些子区间的共同特点是:若区间结尾为R，则区间长度就等于R的二进制分解下最小的2的次幂，即$lowbit(R)$

例如:$x = 7 = 2^2 + 2 ^ 1 + 2 ^ 0$，那么查询区间[1, 7]就可以划分为查询$[1, 4]$、$[5, 6]$、$[7, 7]$三个不重复子区间，
区间长度分别是$lowbit(4) = 4$，$lowbit(6) = 2$，$lowbit(7) = 1$。

对于一个长度为N的序列$a$，我们建立一个同样长度为N的树状数组$tree$，其中$tree[x]$保存序列$a$的区间$[x - lowbit(x) + 1, x]$中所有数的和，即$\sum_{i=x-lowbit(x)+1}^{x}a[i]$。树状数组结构如下图所示：

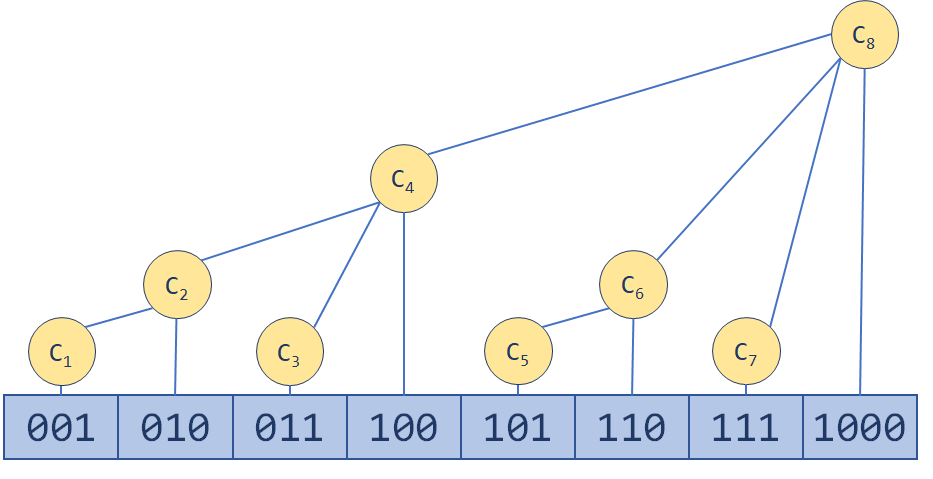
该结构满足以下性质：

1. 每个内部节点$tree[x]$保存以它为根的子树中所有节点的和
2. 每个内部节点$tree[x]$的子节点个数等于$lowbit(x)$的位数
3. 除树根外，每个内部节点$tree[x]$的父节点是$tree[x + lowbits(x)]$
4. 树的深度是$O(\log_2N)$

单点更新(update)

单点更新就是把原序列中的一个数$a[x]$加上一个$\Delta u$，同时正确维护树状数组所记录的区间和。

根据上面给出的树状数组树形结构和它的性质，不难发现只有$tree[x]$及其所有祖先节点保存的区间和包含$a[x]$，
因此就像“爬树”一样，从$tree[x]$开始每次下标$+lowbit(x)$寻找到祖先节点，逐一进行更新即可。

查询前缀和(query)

查询前缀和，即序列$a$中第$1 \sim x$个数的和。

按照我们上述提出的方法，应该求出x的二进制表示的每个等于1的位，把$[1, x]$分为$O(\log N)$个不重复子区间，而每个子区间的区间和都已经保存在树状数组$tree$中，把这些子区间的区间和加起来就能在$O(\log N)$ 的时间内查询前缀和。

---

1-based树状数组板子如下：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1e5 + 7;

struct BinaryIndexTree {
    int tr[N];
   	int lowbit(int x) {
        return x & -x;
    }
    void update(int x, int d) {
        for (; x < N; x += lowbit(x)) tr[x] += d;
    }
    int query(int x) {
        int res = 0;
        for (; x; x -= lowbit(x)) res += tr[x];
        return res;
    }
};

int main() {
    int n;
    cin >> n;
    
    int a[N];
    BinaryIndexTree bit;
    memset(bit.tr, 0, sizeof bit.tr);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        bit.update(i, a[i]); // 构建树状数组
    }
    int l, r;
    cin >> l >> r;
    cout << bit.query(r) - bit.query(l - 1); //查询区间和[l, r]
    
    return 0;
}

个人认为树状数组是要比ST表好理解不少的。

复杂度分析

• 时间复杂度：
  • 构建：$O(n \log n)$，构建相当于是做n次单点更新
  • 单点更新：$O(\log n)$
  • 查询区间和：$O(\log n)$
• 空间复杂度：$O(n)$

拓展

树状数组维护最值

没想到吧～(∠・ω< )⌒☆，树状数组也能维护最值，简直是叹为观止！

单点更新(update)

单点更新操作与前缀和是一样的，只有$tree[x]$及其所有祖先节点保存的区间和包含$a[x]$，逐一更新即可。

查询最值(query)

查询区间最值和查询前缀和操作不太一样：区间$[l, r]$前缀和是用$[1, r]$的前缀和减去$[1, l - 1]$的前缀和。

显然区间最值是没有这个性质的，所以只能换个思路：

由定义：$tr[r]$表示的是$[r - lowbit(r) + 1, r]$，我们就要不断缩小$r$使$r - lowbit(r) + 1$逼近$l$

当$r - lowbit(r) + 1 \ge l$时，$[l, r]$完全覆盖$[r - lowbit(r) + 1, r]$，$res = max(query(l, r - lowbit(r), tr[r])$

当$r - lowbit(r) + 1 < l$时，分离$a[r]$，让$r$减$1$使$r - lowbit(r) + 1$逼近$l$，$res = max(query(l, r - 1), a[r])$

写成递归形式：

int query(int l, int r) {
    if (l > r) return 0;
    int res = 0;
    if (r - lowbit(r) + 1 >= l) res = max(query(l, r - lowbit(r)), tr[r]);
    if (r - lowbit(r) + 1 < l) res = max(query(l, r - 1), a[r]); 
    return res;
}

写成递推形式：

int query(int l, int r) {
    int res = 0;
    while (l <= r) {
        res = max(res, a[r]); r--;
        for (; r - lowbit(r) >= l; r -= lowbit(r)) res = max(res, tr[r]);
    }
    return res;
}

• 时间复杂度：$O (\log^2 n)$，因为$r$经过$\log n$次变换后，其与$l$不同的最高位至少会下降1位，所以最多进行$(\log^2 n)$次变换

---

下面给出树状数组维护区间最值的板子：

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1e5 + 7;

struct BinaryIndexTree {
    int tr[N], a[N];
    int lowbit(int x) {
        return x & -x;
    }  
    void update(int x, int v) {
        for (; x < N; x += lowbit(x)) tr[x] = max(tr[x], v);
    }
    int query(int l, int r) {
        int res = 0;
        while (l <= r) {
            res = max(res, a[r]); r--;
            for (; r - lowbit(r) >= l; r -= lowbit(r)) res = max(res, tr[r]);
        }
        return res;
    }
};

int main() {
    int n;
    cin >> n;
    
    BinaryIndexTree bit;
    memset(bit.tr, 0, sizeof bit.tr);
    memset(bit.a, 0, sizeof bit.a);
    for (int i = 1; i <= n; i++) {
        cin >> bit.a[i];
        bit.update(i, bit.a[i]); // 构建树状数组
    }
    int l, r;
    cin >> l >> r;
    cout << bit.query(l, r); //查询区间[l, r]的最值
    
    return 0;
}

差分树状数组

todo：差分树状数组，可用于区间更新+单点查询

练习eg:

Acwing-107. 求逆序对

LeetCode-2407. 最长递增子序列II