RetinaNet

RetinaNet

Introduction

论文题目 : ReDet:A Rotation-equivariant Detector for Aerial Object Detection

论文地址 : https://arxiv.org/pdf/1708.02002.pdf

Focal Loss用于解决类别不均衡问题，从而创造了RetinaNet（One Stage目标检测算法）这个精度超越经典Two Stage的Faster-RCNN的目标检测网络。

Idea

基于深度学习的目标检测算法有两类经典的结构：Two Stage 和 One Stage。

Two Stage(1-2k)：例如Faster-RCNN算法。第一阶段专注于proposal的提取，第二阶段对提取出的proposal进行分类和精确坐标回归。两级结构准确度较高，但因为第二级需要单独对每个proposal进行分类/回归，速度上就打了折扣。

One Stage(~100k): 例如SSD，YOLO算法。此类算法摒弃了提取proposal的过程，只用一级就完成了识别/回归，虽然速度较快但准确率远远比不上两级结构。

产生精度差异的主要原因：类别失衡（Class Imbalance）。One Stage方法在得到特征图后，会产生密集的目标候选区域，而这些大量的候选区域中只有很少一部分是真正的目标，这样就造成了机器学习中经典的训练样本正负不平衡的问题。它往往会造成最终算出的training loss为占绝对多数但包含信息量却很少的负样本所支配，少样正样本提供的关键信息却不能在一般所用的training loss中发挥正常作用，从而无法得出一个能对模型训练提供正确指导的loss（而Two Stage方法得到proposal后，其候选区域要远远小于One Stage产生的候选区域，因此不会产生严重的类别失衡问题）。该论文中提出了Focal Loss来降低类别失衡，对最终的Loss进行校正。

Network

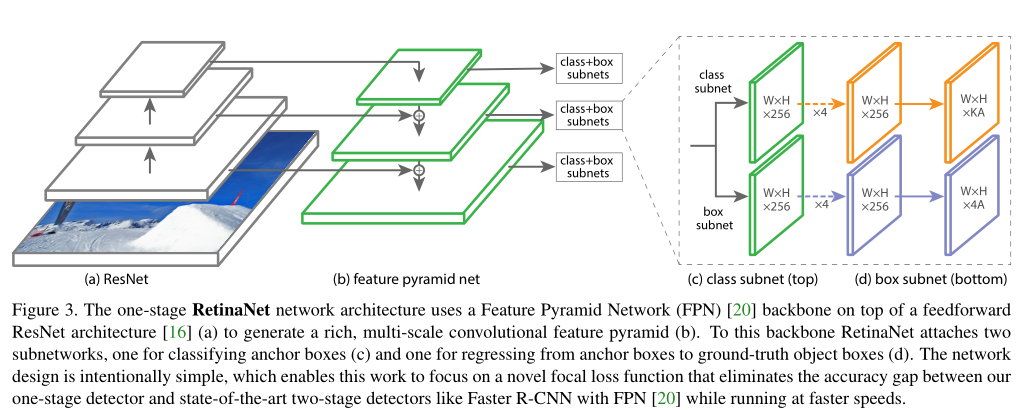
RetinaNet的网络结构: ResNet + FPN + FCN*2

输入图像经过Backbone的特征提取后，可以得到P3{P_3}~P7{P_7}特征金字塔，对每层特征金字塔分别使用两个子网络（分类网络+检测框位置回归）。

子网络的设计类似于RPN，使用anchors来产生proposal。

上面说到的Focal Loss就应用于类别分类的子网络，即可有效移植类别不均衡问题。

特征金字塔每层都相应的产生目标类别与位置的预测，最后再将其融合起来，同时使用NMS来得到最后的检测结果。

Focal Loss

Focal Loss这个trick主要是在交叉熵损失函数做改进。

对于一般的二分类问题，其交叉熵损失函数如下:

CE(p,y)=L(y,p)=−ylog(p)−(1−y)log(1−p){CE(p,y) = L(y,p) = -ylog(p) - (1-y)log(1-p)}

可以写成:

CE={−log⁡(p) if y=1−log⁡(1−p) if y=−1(otherwise)CE= \begin{cases} -\log_{}{(p)} & \text{ if } y=1 \\ -\log_{}{(1-p)} & \text{ if } y=-1(otherwise) \end{cases}

为了方便，定义pt{p_t}表示pp，如下:

pt={p if y=11−p if y=−1(otherwise)p_t= \begin{cases} p & \text{ if } y=1 \\ 1-p & \text{ if } y=-1(otherwise) \end{cases}

这样CE就可以表示成如下表达式:

CE(p,y)=CE(pt)=−log⁡ptCE(p,y) = CE(p_t) = -\log{}{p_t}

pt可以看作样本被正确分类的一个概率值。

可以认为当模型预测得到的 Pt>0.5P_t > 0.5的样本为easy examples ; 而PtP_t值预测较小的样本为hard examples。

Postive/Negative example

解决class imbalance的一个方法是为类1添加一个权重因子α ∈ [0, 1]，对于y =1的使用权重 α ，对y =-1使用 1-α；这样就能一定程度上的解决了正负样本的不平衡。

CE=−αlog⁡pt={−αlog⁡(p) if y=1−(1−α)log⁡(1−p) if y=−1(otherwise)CE= -\alpha \log_{}{p_t}= \begin{cases} -\alpha \log_{}{(p)} & \text{ if } y=1 \\ -(1-\alpha)\log_{}{(1-p)} & \text{ if } y=-1(otherwise) \end{cases}

Easy/Hard example

因为hard examples通常为少数样本，所以虽然其对应的loss值较高，但是最后全部累加后，大部分的loss值来自于容易分类的样本，这样在模型优化的过程中就会将更多的优化放到容易分类的样本中，而忽略hard examples。因此论文中引入调节因子(1−pt)γ(1-p_t)^{\gamma}

CE=−(1−pt)γlog⁡pt={−(1−p)γlog⁡(p) if y=1−pγlog⁡(1−p) if y=−1(otherwise)CE= -(1-p_t)^{\gamma} \log_{}{p_t}= \begin{cases} -(1-p)^{\gamma} \log_{}{(p)} & \text{ if } y=1 \\ -p^{\gamma}\log_{}{(1-p)} & \text{ if } y=-1(otherwise) \end{cases}

PtP_t较大时为Easy example，此时调制因子接近0, 降低了Loss累加中Easy example的权重;

PtP_t较小时为Hard example，此时调制因子接近1, 增加了Loss累加中Easy example的权重。

通过实验测试，超参数γ=2\gamma = 2效果最好。

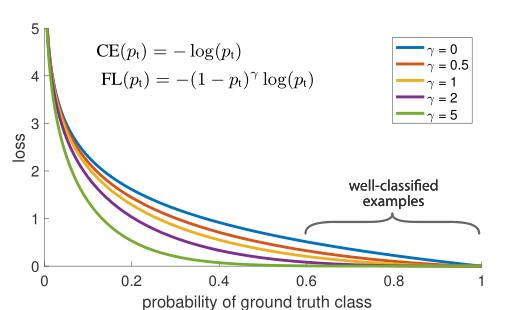
将上述两种权重因子整合起来，就是最终的Focal Loss:

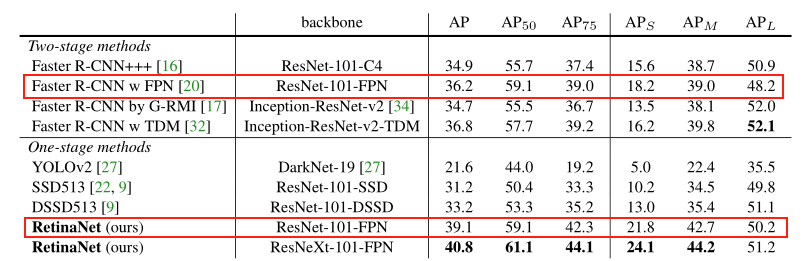
CE=−α(1−pt)γlog⁡pt={−α(1−p)γlog⁡(p) if y=1−(1−α)pγlog⁡(1−p) if y=−1(otherwise)CE= -\alpha(1-p_t)^{\gamma} \log_{}{p_t}= \begin{cases} -\alpha(1-p)^{\gamma} \log_{}{(p)} & \text{ if } y=1 \\ -(1-\alpha)p^{\gamma}\log_{}{(1-p)} & \text{ if } y=-1(otherwise) \end{cases}

下图是论文中给出的试验结果，相比较于经典的Two Stage检测方法Faster-RCNN，RetinaNet具有更高的精度。