GWD Loss

Gaussian Wasserstein Distance Loss

Introduction

论文题目 : Rethinking Rotated Object Detection with GaussianWasserstein Distance Loss

论文地址 : https://arxiv.org/pdf/2101.11952v4.pdf

Idea

将任意旋转矩形近似成一个二维的高斯分布，通过计算分布之间的Wasserstein距离解决RIoU不可导的问题

目前旋转目标检测主流的工作，相较于水平目标检测，都是添加一个角度参数，采用回归的方法来预测旋转角度。但是这样的角度回归模型会带来新的问题：

  1. 评估度量（metric）和损失（loss）和的不一致性
  2. 边界不连续性
  3. 类正方形检测问题

Detail

先认识上述提到的三个问题

The inconsistency between metric（IOU） and loss

IOU一直是水平和旋转目标检测的标准评估指标，然而该度量和回归损失之间存在着不一致。

在水平目标检测中,后面提出的PIOU和DIOU可以填补这个问题，但是在旋转目标检测中，两个旋转框的IOU的Learning是不可微分的(旋转IoU存在稀疏的几个不可导点)

作者举例提到了一个(ln-norms)，并给出了论文索引[45,80]，还没深究。

而旋转目标检测的角度回归模型，更放大了这一特性:

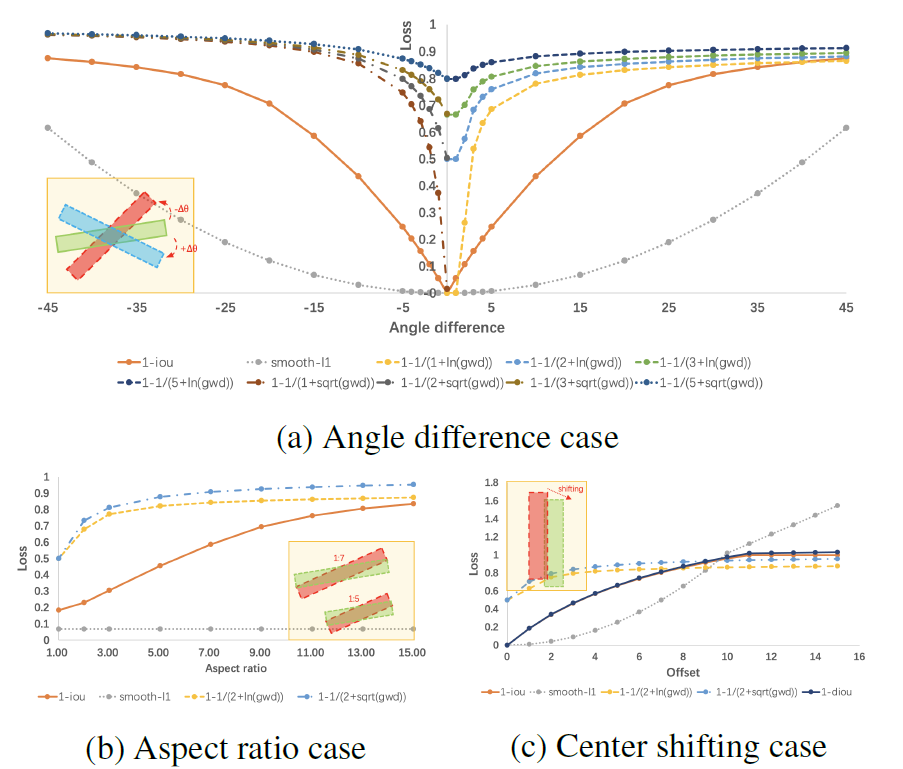
主要看图中IOU和经典旋转目标检测中的Smooth L1 Loss的对比

  1. 图a描述了角度差和损失函数的关系
  2. 图b展示了具有不同的长宽比例的检测框和损失函数的关系
  3. 图c探讨了中心点移动和损失函数的关系

通过以上对比，可以看出旋转目标检测中经典的Smooth L1 loss的缺陷。

Boundary discontinuity

两种定义方法:长边定义法和OpenCV定义法。

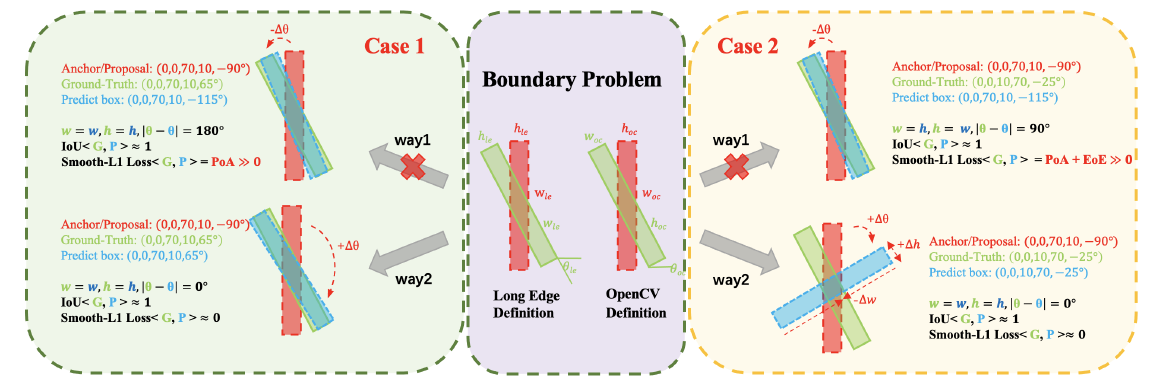
这里的边界问题主要在于预定义的anchor/proposal如果在90度,180度等这样的边界位置，

长边定义法在边界处有角度的周期性(POA)

OpenCV定义法在边界处有角度的周期性(POA)和长短边的可交换性(EOE)

导致预测框的结果超出了定义范围，此时会带来非常大的Smooth L1 IOU Loss。

这对一些学习能力较弱的模型，在边界情况下的表现是非常脆弱的:

Square-like problem

基于长边定义法的模型还存在一个类似正方形的对象检测问题。

预测框(-60度)和Ground Truth(30度)的IOU接近1，但是回归损失会很大，这样又回到了第一个问题:评估度量和损失的不一致。

而由于OpenCV定义法具有长短边的可交换性，因此不存在类Square-like problem。

The Proposed Method

将任意旋转矩形近似成一个二维的高斯分布，通过计算分布之间的Wasserstein距离解决RIoU不可导的问题

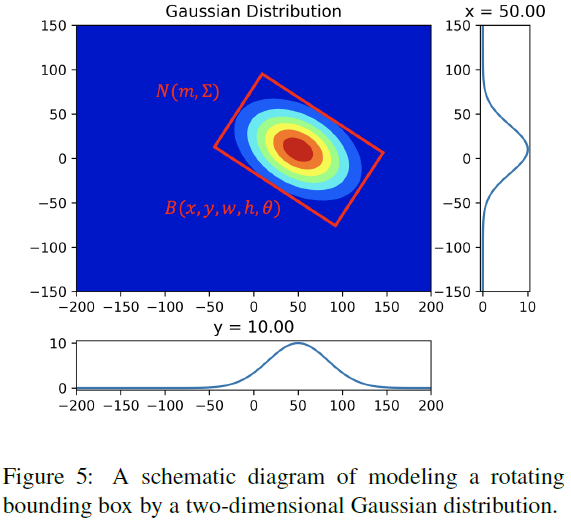
将任意旋转矩形框转换为二维高斯分布:

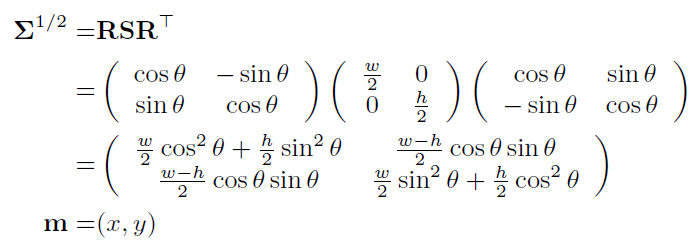
两个高斯分布之间的Wasserstein距离公式:

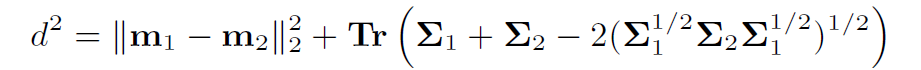
而该Wasserstein距离是可导的，这样通过计算两个高斯分布之间Wasserstein距离的Loss来近似IOU的Loss

后续通过引入一些超参数变换，控制函数值域，去近似IOU的Loss：

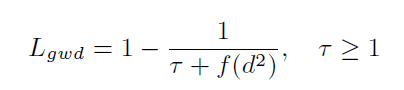
Result

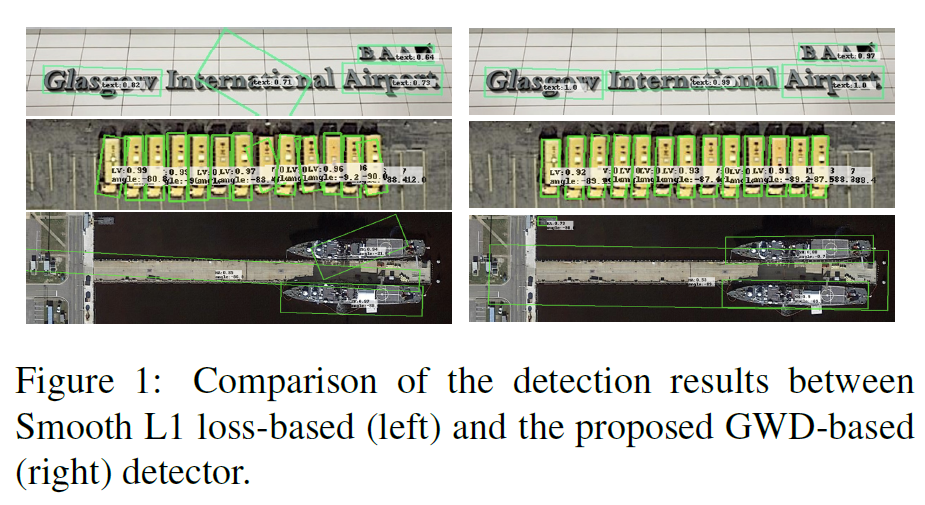
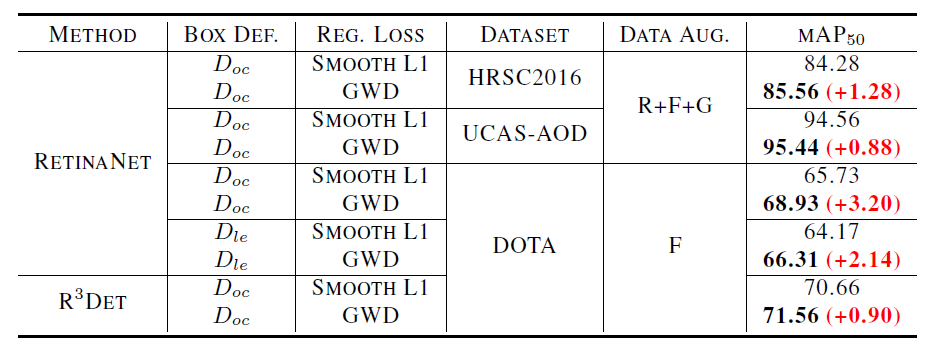
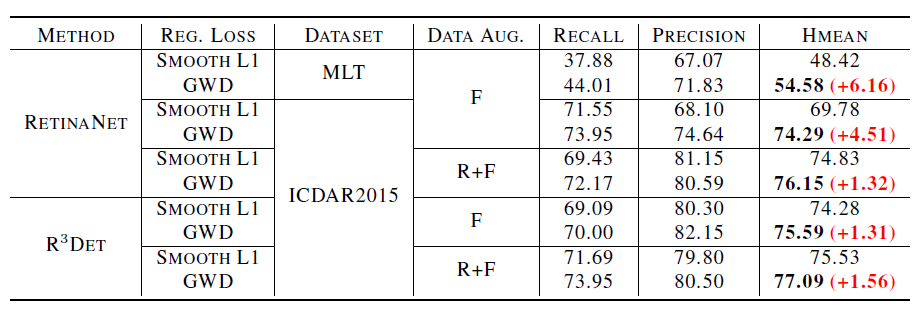
作者在五个公共数据集和两个前沿的旋转目标检测模型上，应用了该GWD Loss，得到的效果基本完胜IoU-Smooth L1 Loss, Modulated loss，CSL, 和DCL。