Localization Distillation
Localization Distillation for Dense Object Detection
Introduction
论文题目 :Localization Distillation for Dense Object Detection
论文地址 :https://arxiv.org/pdf/2102.12252.pdf
论文出处 :2022’CVPR
代码实现 :https://github.com/HikariTJU/LD
Idea
把用于分类的KD(Knowledge Distillation),用于回归BBox中,形成了LD(Localization Distillation)。
做法:先把bbox的4个logits输出值,离散化成4n个logits输出值,之后与分类KD几乎一致。
Detail
Logits Distillation
参考文献⏬
现在的深度学习模型越来越大,尤其是近年Transformer比较火,而各种基于的Transformer的模型参数普遍较多,在这种情况下就需要找到有效的模型压缩的方法。知识蒸馏就又回归到了研究者的视野之中。
KD最早就是专门为图像分类而设计的:
核心思想:就是用一个已训练的复杂模型(Teacher,黑盒)输出的知识,去指导一个小模型(Student)训练学习。
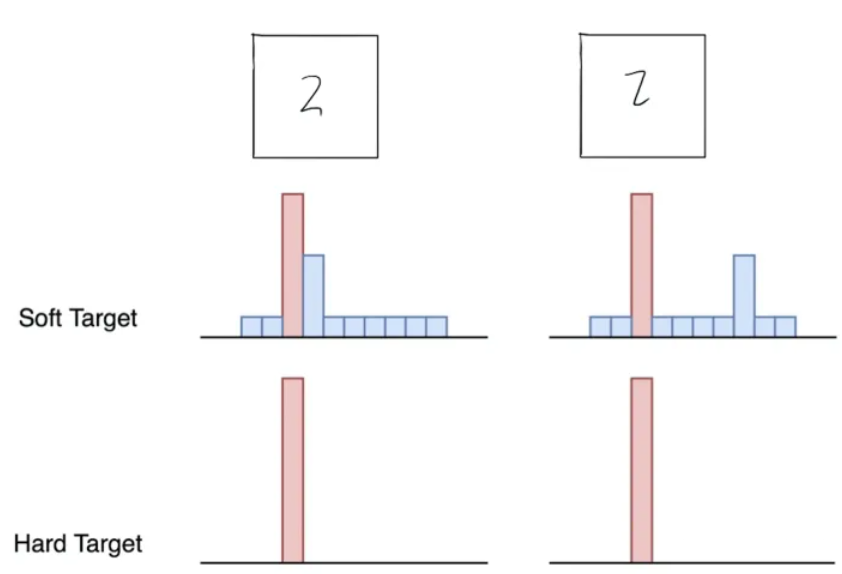
知识:soft targets和hard targets
分类采用的是one-hot编码:
hard targets: Ground truth <=> 极大似然
soft targets: Softmax层输出 <=> 概论分布
softmax层的输出,除了正例之外,负标签也带有大量的信息,比如某些负标签对应的概率远远大于其他负标签。而在传统的训练过程(hard target)中,所有负标签都被统一对待。
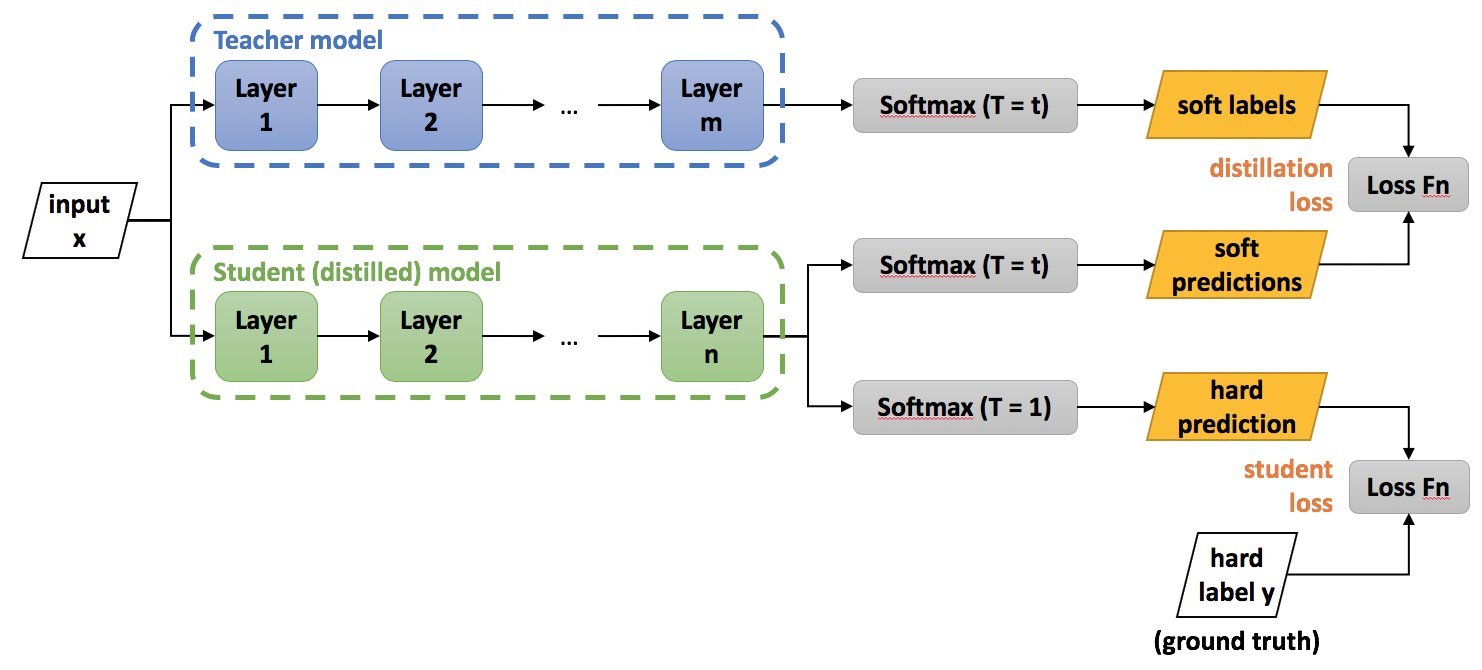
蒸馏:温度T
但是原始softmax函数的负标签概率都接近0,对损失函数的贡献非常小。
当T=1时,就是原始softmax函数,T越高,标签越平滑,负标签携带的信息会被相对地放大
T = 100,标签更平滑
distill loss
在温度T的条件下,student的softmax输出和teacher输出的soft target的cross entropy就是Loss函数的第一部分
其中
在温度T=1的条件下,student的softmax输出和ground truth的cross entropy就是Loss函数的第二部分
其中
上述公式中:
- :Teacher模型中的logits(logits是softmax之前,网络中最后一个全连接层的输出)
- : student模型中的logits
- :Teacher模型在温度T下的softmax输出在第i类上的值
- :student模型在温度T下的softmax输出在第i类上的值
- : ground truth在第i类上的值,正标签取1,负标签取0
- : 总标签的数量
目前知识蒸馏主要分为了两个派系:logit蒸馏和feature蒸馏,上述是logit蒸馏
Localization Distillation
基于此背景,再说说本文的LD,LD想解决的问题与GFL一样–由遮挡等因素带来的定位不确定性

参考GFL,假设bbox的边e
然后把range离散化为集合。
集合中的每个值可以看作一个类,一般取间隔为1。
这样bbox的每条边都可以通过Softmax函数转为一个概率分布。
作者使用的是相对熵(KL-divergence)作为LD的概率:
其中,符号基本与上文对应。
也算是把KD和LD的任务统一了,统称为Logit Mimicking。
others
后续作者结合了feature蒸馏只会传递混合知识的,划分了两个区域:
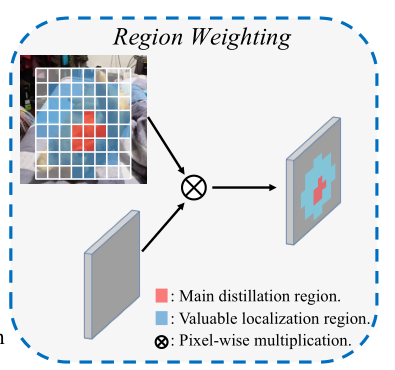
- Main distillation Region(主蒸馏区域、红色)<=> 直接通过正标签的所在区域确定
- Valuable Localization Region(有价值区域,蓝色) <=> 通过设置DIOU阈值,计算DIOU确定
讨论了分别在Main,VLR区域中使用KD、LD的效果消融实验:
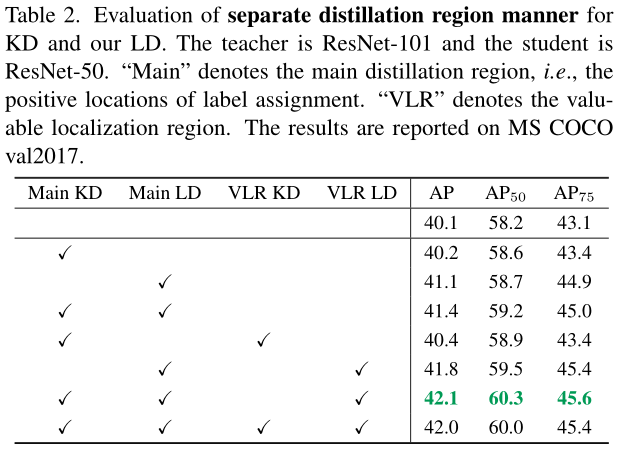
由于不太了解feature蒸馏,所以这一部分没细看。
总结
我认为蒸馏不是本文的重点,
倒是最近这种通过离散化,然后加权(概率),把bbox的回归任务看成分类任务的思想比较常见。
本博客所有文章均采用 CC BY-NC-SA 4.0 协议 ,禁止商用,转载请注明出处!