题目链接

算法竞赛进阶指南-37.数的进制转换

编写一个程序，可以实现将一个数字由一个进制转换为另一个进制。

这里有 $62$ 个不同数位 $\{0-9,A-Z,a-z\}$。

输入格式

第一行输入一个整数，代表接下来的行数。

接下来每一行都包含三个数字，首先是输入进制（十进制表示），然后是输出进制（十进制表示），最后是用输入进制表示的输入数字，数字之间用空格隔开。

输入进制和输出进制都在 $2$ 到 $62$ 的范围之内。

（在十进制下）$A = 10，B = 11，…，Z = 35，a = 36，b = 37，…，z = 61$ ($0-9$ 仍然表示 $0-9$)。

输出格式

对于每一组进制转换，程序的输出都由三行构成。

第一行包含两个数字，首先是输入进制（十进制表示），然后是用输入进制表示的输入数字。

第二行包含两个数字，首先是输出进制（十进制表示），然后是用输出进制表示的输入数字。

第三行为空白行。

同一行内数字用空格隔开。

输入样例：

8
62 2 abcdefghiz
10 16 1234567890123456789012345678901234567890
16 35 3A0C92075C0DBF3B8ACBC5F96CE3F0AD2
35 23 333YMHOUE8JPLT7OX6K9FYCQ8A
23 49 946B9AA02MI37E3D3MMJ4G7BL2F05
49 61 1VbDkSIMJL3JjRgAdlUfcaWj
61 5 dl9MDSWqwHjDnToKcsWE1S
5 10 42104444441001414401221302402201233340311104212022133030

输出样例：

62 abcdefghiz
2 11011100000100010111110010010110011111001001100011010010001

10 1234567890123456789012345678901234567890
16 3A0C92075C0DBF3B8ACBC5F96CE3F0AD2

16 3A0C92075C0DBF3B8ACBC5F96CE3F0AD2
35 333YMHOUE8JPLT7OX6K9FYCQ8A

35 333YMHOUE8JPLT7OX6K9FYCQ8A
23 946B9AA02MI37E3D3MMJ4G7BL2F05

23 946B9AA02MI37E3D3MMJ4G7BL2F05
49 1VbDkSIMJL3JjRgAdlUfcaWj

49 1VbDkSIMJL3JjRgAdlUfcaWj
61 dl9MDSWqwHjDnToKcsWE1S

61 dl9MDSWqwHjDnToKcsWE1S
5 42104444441001414401221302402201233340311104212022133030

5 42104444441001414401221302402201233340311104212022133030
10 1234567890123456789012345678901234567890

Method : 高精度

A=>10=>B

因为int的输出默认就是10进制表示的，因此很好写

秦九韶算法： A进制 => 10进制

$(101010)_2=1 * 2^5+0 * 2^4+1 * 2^3+0 * 2^2+1 * 2^1+0 * 2^0=(42)_2$

vector<int> arr;
long long res = 0; // 这里要考虑用64位整形能否存得下
for (int i = 0; i < arr.size(); i ++) {
	res = res * A + arr[i];
}

短除法 : 10进制 => B进制

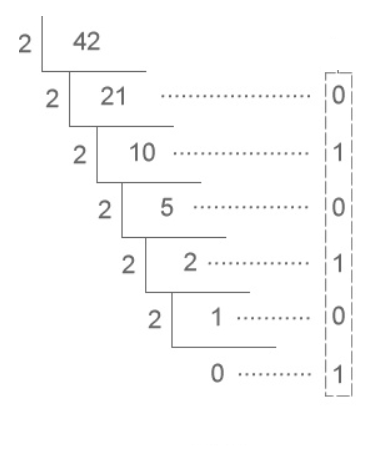
vector<int> res;
for (; n; n /= b) {
	res.push_back(n % B);
}
// 此时res是倒序存储的
reverse(res.begin(), res.end());

A=>B

可以直接 短除法 + 高精度除法模拟，实现从A进制转换到B进制

#include <vector>
#include <string>
#include <iostream>
#include <algorithm>

using namespace std;

int to_num(char c) {
    if ('0' <= c && c <= '9') return c - '0';
    if ('A' <= c && c <= 'Z') return c - 'A' + 10;
    if('a' <= c && c <= 'z') return c - 'a' + 36;
}

char to_char(int n) {
    if (0 <= n && n <= 9) return n + '0';
    if (10 <= n && n <= 35) return n - 10 + 'A';
    if(36 <= n && n <= 61) return n - 36 + 'a';
}

string trans(string in_num, int in, int out) {
    string out_num;

    while (in_num.size()) {
        int r = 0; // 余数
        // 直接从高位开始处理
        for (int i = 0; i < in_num.size(); i ++) {
             int num_i = to_num(in_num[i]);
             num_i = r * in + num_i;
             in_num[i] = to_char(num_i / out); // 商
             r = num_i % out; //余数
        }
        out_num += to_char(r);

        // 去掉高位的0
        while (in_num.size() && in_num.front() == '0') in_num.erase(0, 1);
    }

    reverse(out_num.begin(), out_num.end());
    return out_num;
}

int main() {
    int T;
    cin >> T;

    while (T --) {
        int in, out;
        string in_num;
        cin >> in >> out;
        cin >> in_num;

        string out_num = trans(in_num, in, out);

        cout << in << " " << in_num << endl;
        cout << out << " " << out_num << endl;
        puts("");
    }

    return 0;
}

复杂度分析

• 时间复杂度${O(T * C *n)}$， 很难确定，因为$trans$函数的while循环的迭代次数与$in$和$out$进制相关，因此用了一个大常数$C$表示，而且本题也不太需要考虑时间复杂度，只需要保证转换后的正确性即可。

• 空间复杂度${O(n)}$。

记录一下思考过程~

#include <vector>
#include <string>
#include <iostream>
#include <algorithm>

using namespace std;

// vector<int> div(vector<int> &A, int b, int &r, int base) {
//     vector<int> C;
    
//     r = 0;
//     // 从高位处理
//     for (int i = A.size() - 1; i >= 0; i --) {
//         r = r * base + A[i];
//         C.push_back(r / b);
//         r %= b;
//     }
    
//     reverse(C.begin(), C.end());
//     while (C.size() > 1 && C.back() == 0) C.pop_back();
//     return C;
// }

int to_num(char c) {
    if ('0' <= c && c <= '9') return c - '0';
    if ('A' <= c && c <= 'Z') return c - 'A' + 10;
    if('a' <= c && c <= 'z') return c - 'a' + 36;
}

char to_char(int n) {
    if (0 <= n && n <= 9) return n + '0';
    if (10 <= n && n <= 35) return n - 10 + 'A';
    if(36 <= n && n <= 61) return n - 36 + 'a';
}

string trans(string in_num, int in, int out) {
    string out_num;
    
    while (in_num.size()) {
        int r = 0; // 余数
        for (int i = 0; i < in_num.size(); i ++) {
             int num_i = to_num(in_num[i]);
             num_i = r * in + num_i;
             in_num[i] = to_char(num_i / out); // 商
             r = num_i % out; //余数
            //  cout << num_i << endl;
        }
        // cout << "------" << endl;
        out_num += to_char(r);
        
        // 去掉高位的0
        while (in_num.size() && in_num.front() == '0') in_num.erase(0, 1);
        
        // 去掉高位的0
        // reverse(in_num.begin(), in_num.end());
        // while (in_num.size() && in_num.back() == '0') in_num.pop_back();
        // reverse(in_num.begin(), in_num.end());
    }
    
    // cout << "----" << endl;
    // 直接从高位开始处理
    // for (int i = 0 ; i < in_num.size(); i ++) {
    //     int num_i = to_num(in_num[i]);
        
    //     // cout << num_i << endl;
    //     // r = r * in + num_i;
    //     // out_num.push_back(to_char(r / out));
    //     // r %= out;
    // }
    
    // while (out_num.size() > 1 && out_num.back() == 0) out_num.pop_back();
    reverse(out_num.begin(), out_num.end());
    
    return out_num;
}

int main() {
    int T;
    cin >> T;
    
    while (T --) {
        int in, out;
        string in_num;
        // scanf("%d %d ", &in, &out);
        // cin >> in_num;
        cin >> in >> out;
        // getchar();
        cin >> in_num;
        
        
        string out_num = trans(in_num, in, out);
        
        // cout << in_num << endl;
        cout << in << " " << in_num << endl;
        cout << out << " " << out_num << endl;
        puts("");
    }
    
    return 0;
}