论文分享

QPDet

Quadrant Point Representation

象限点表达方式:

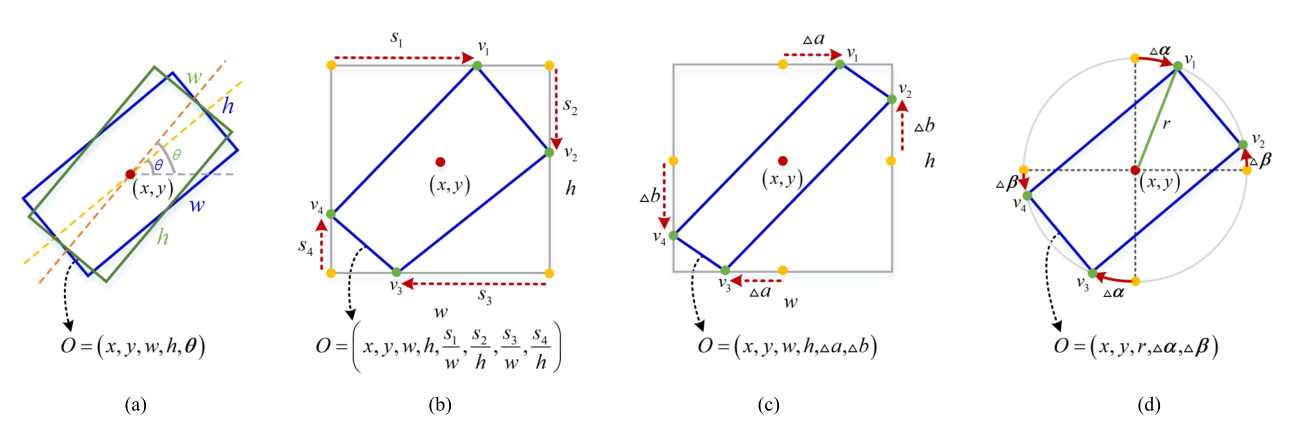
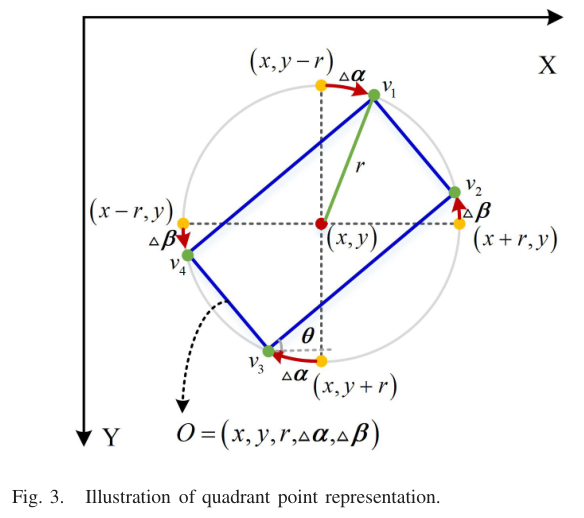
$r^2 = (w/ 2) ^ 2 + (h / 2) ^ 2$

$\Delta \alpha$ 是相对于最上边的点的偏移量， $\Delta \beta$是相对于最右边的点的偏移量 ，都是弧度

$(v_1,v_2,v_3,v_4)$和 ${(x, y, r, \Delta \alpha, \Delta \beta)}$的转换关系：

$\left\{\begin{array}{l}v_1=(x+r \sin (\Delta \alpha), y-r \cos (\Delta \alpha)) \\ v_2=(x+r \cos (\Delta \beta), y+r \sin (\Delta \beta)) \\ v_3=(x-r \sin (\Delta \alpha), y+r \cos (\Delta \alpha)) \\ v_4=(x-r \cos (\Delta \beta), y-r \sin (\Delta \beta))\end{array}\right.$

encoder-decoder编码转换:

$\begin{cases}\delta_x=\left(x^*-x_a\right) / 2 r_a, & \tau_x=\left(x^{\prime}-x_a\right) / 2 r_a \\ \delta_y=\left(y^*-y_a\right) / 2 r_a, & \tau_y=\left(y^{\prime}-y_a\right) / 2 r_a \\ \delta_r=\log \left(r^* / r_a\right), & \tau_r=\log \left(r^{\prime} / r_a\right) \\ \delta_\alpha=\Delta \alpha^*, & \tau_\alpha=\Delta \alpha^{\prime} \\ \delta_\beta=\Delta \beta^*, & \tau_\beta=\Delta \beta^{\prime} .\end{cases}$

Result

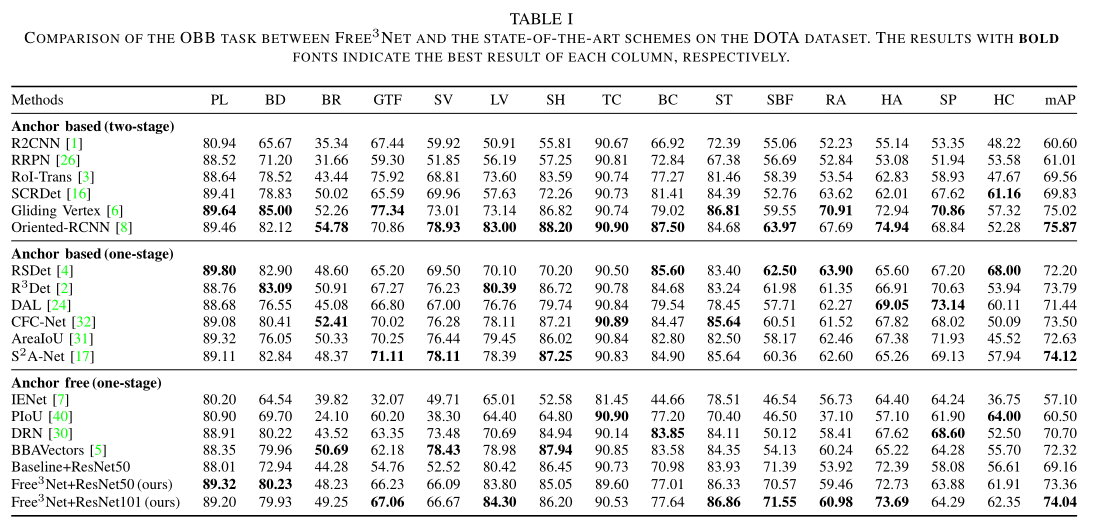
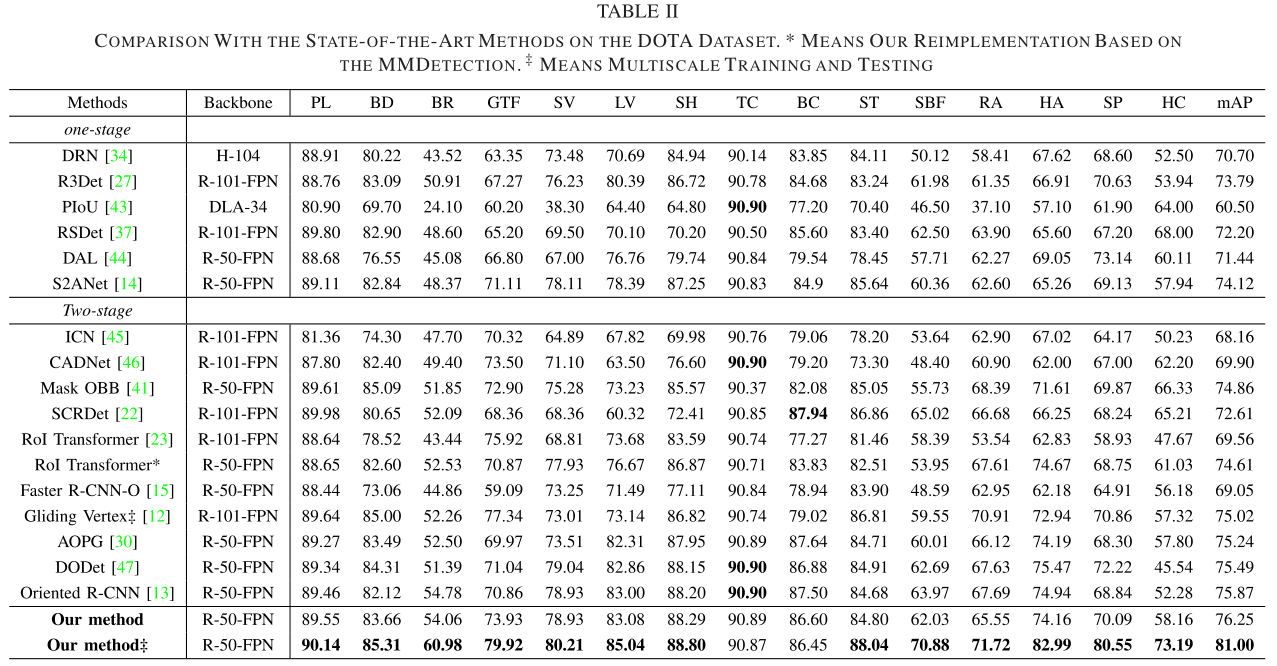
多尺度训练的精度(Backbone都是Res50-FPN,) Oriented-RCNN是80.87, QPDet是81.00.

无多尺度(Res50-FPN) Oriented-RCNN是75.87 ; QPDet是76.25

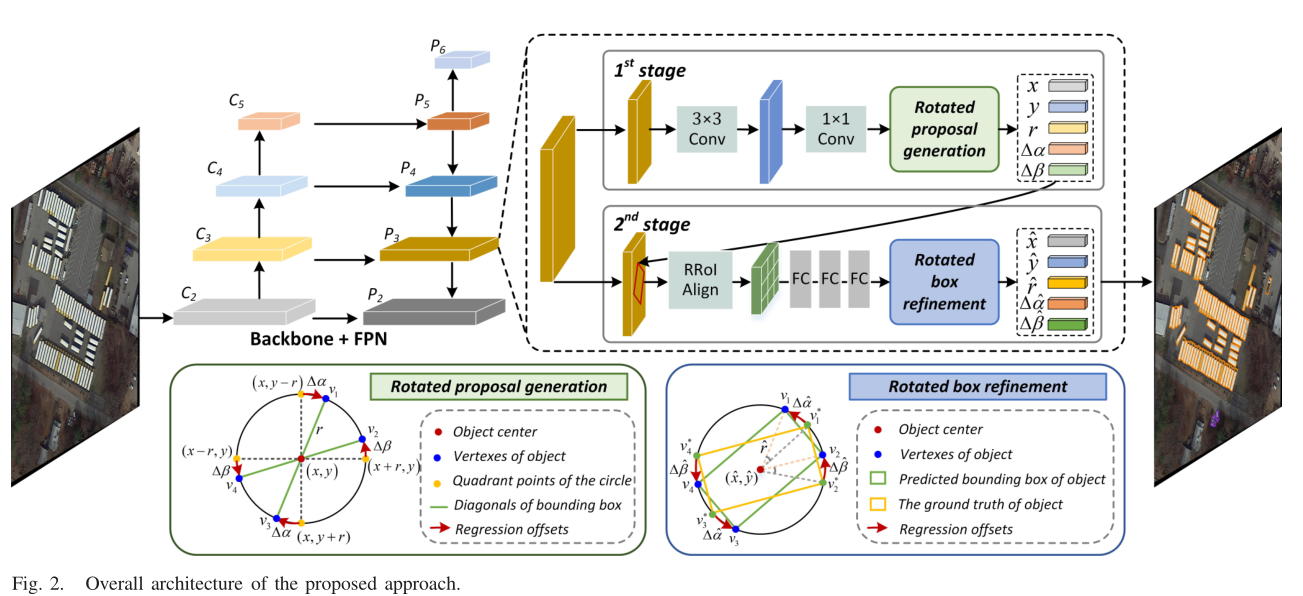
Free3Det

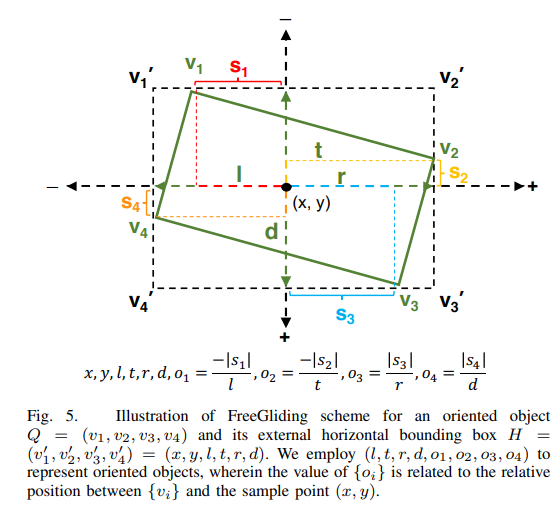
$(x, y)$是一个采样点，而不是中心点

$(l, t, r ,d)$是到外接矩形的距离，就确定了外接矩形的形状

$(o_1, o_2, o_3, o_4)$就能间接表示$(s_1, s_2, s_3, s_4)$，从而确定了旋转矩形框的顶点$(v_1,v_2, v_3, v_4)$

$(v_1,v_2,v_3,v_4)$和 ${(x, y,l, t, r ,d, o_1, o_2, o_3, o_4)}$的转换关系：

$\begin{aligned} & \boldsymbol{v}_{\mathbf{1}}=\left(\left\{\begin{array}{ll}x+o_1 * l, & o_1<0 \\ x+o_1 * r, & o_1 \geq 0\end{array}, \quad y-t\right)\right. \\ & \boldsymbol{v}_{\mathbf{2}}=\left(x+r, \quad\left\{\begin{array}{ll}y+o_2 * t, & o_2<0 \\ y+o_2 * d, & o_2 \geq 0\end{array}\right)\right. \\ & \boldsymbol{v}_{\mathbf{3}}=\left(\left\{\begin{array}{ll}x+o_3 * l, & o_3<0 \\ x+o_3 * r, & o_3 \geq 0\end{array}, \quad y+d\right)\right. \\ & \boldsymbol{v}_{\mathbf{4}}=\left(x-l, \quad\left\{\begin{array}{ll}y+o_4 * t, & o_4<0 \\ y+o_4 * d, & o_4 \geq 0\end{array}\right)\right. \\ & \end{aligned}$

Result

无多尺度(Res50-FPN) 73.36