题目链接

算法竞赛进阶指南-42.编辑器

你将要实现一个功能强大的整数序列编辑器。

在开始时，序列是空的。

编辑器共有五种指令，如下：

1、I x，在光标处插入数值 $x$。
2、D，将光标前面的第一个元素删除，如果前面没有元素，则忽略此操作。
3、L，将光标向左移动，跳过一个元素，如果左边没有元素，则忽略此操作。
4、R，将光标向右移动，跳过一个元素，如果右边没有元素，则忽略此操作。
5、Q k，假设此刻光标之前的序列为 $a_1,a_2,…,a_n$，输出 $max_{1 \le i \le k}S_i$，其中 $S_i=a_1+a_2+…+a_i$。

输入格式

第一行包含一个整数 $Q$，表示指令的总数。

接下来 $Q$ 行，每行一个指令，具体指令格式如题目描述。

输出格式

每一个 Q k 指令，输出一个整数作为结果，每个结果占一行。

数据范围

$1 \le Q \le 10^6$,
$|x| \le 10^3$,
$1 \le k \le n$

输入样例：

8
I 2
I -1
I 1
Q 3
L
D
R
Q 2

输出样例：

2
3

Method : 对顶栈

P2201.数列编辑器

维护一个如下图所示的对顶栈，来模拟光标移动：

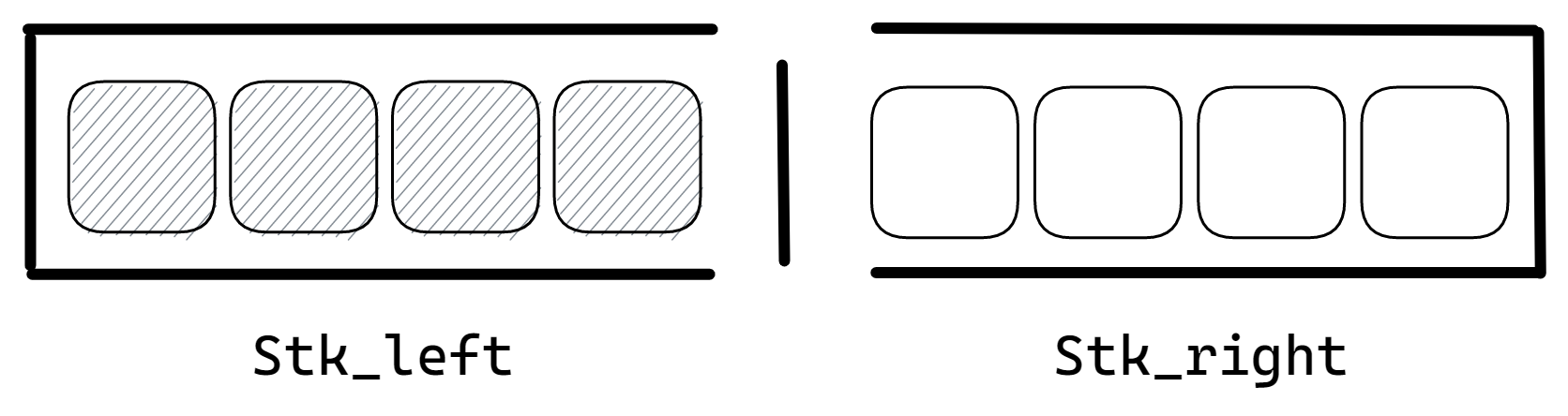
算前缀和的最大值，可以用来动态规划f + idx来写。

#include <string>
#include <vector>
#include <stack>
#include <iostream>

using namespace std;

const int N = 1e6 + 7;
const int INF = 0x3f3f3f3f;

stack<int> stk_l;
stack<int> stk_r;
vector<int> sum(N, 0);
vector<int> f(N, 0);
int idx = 0; // 光标位置

int main() {
    f[0] = -INF;

    int Q;
    cin >> Q;

    while (Q --) {
        string op;
        cin >> op;

        if (op == "I") {
            int x;
            scanf("%d", &x);
            stk_l.push(x);

            idx ++;
            sum[idx] = sum[idx - 1] + stk_l.top();
            f[idx] = max(f[idx - 1], sum[idx]);
        }
        else if (op == "D") {
            if (!stk_l.empty()) {
                stk_l.pop();

                idx --;
            }
        }
        else if (op == "L") {
            if (!stk_l.empty()) {
                int x = stk_l.top();
                stk_l.pop();
                stk_r.push(x);

                idx --;
            }
        }
        else if (op == "R") {
            if (!stk_r.empty()) {
                int x =stk_r.top();
                stk_r.pop();
                stk_l.push(x);

                idx ++;
                sum[idx] = sum [idx - 1] + stk_l.top();
                f[idx] = max(f[idx - 1], sum[idx]);
            }
        }
        else if (op == "Q") {
            int k;
            scanf("%d", &k);
            printf("%d\n", f[k]);
        }
    }

    return 0;
}

复杂度分析

• 时间复杂度：${O(1)}$， 五个操作都是$O(1)$的。

• 空间复杂度：${O(N)}$。