ARS-DETR

Introduction

论文题目 ：ARS-DETR: Aspect Ratio Sensitive Oriented Object Detection with Transformer

论文地址 ：https://arxiv.org/abs/2303.04989v1

论文出处 ：arxiv 2023.03

代码实现 ：https://github.com/httle/ARS-DETR

Idea

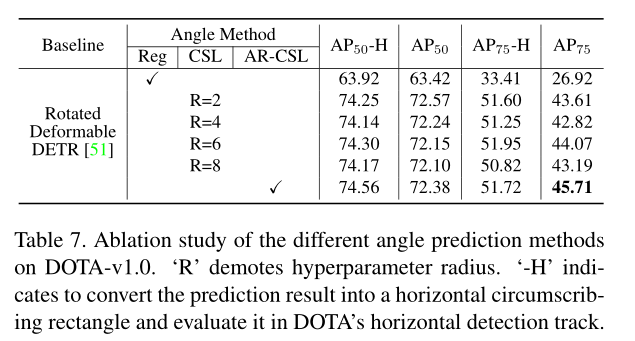
作者认为AP50对角度偏差的容忍度较大，因此使用AP75来衡量模型性能。

作者提出了一种基于Tansformer的横纵比敏感的检测器，具体而言：

1. 提出了一种新的角度分类方法，称为AR-CSL(是此前提出的CSL的改进版本)，以更合理的方式平滑角度标签。
2. 设计了一个旋转可变注意力模块，以相同的角度旋转采样点，来消除采样区域特征和采样点之间的错位。
3. 另外，根据目标的横纵比，来动态调整权重系数计算角度损失。

Detail

AR-CSL

CSL将角度划分为180个类别，并且将第一个角度和最后一个角度视为相邻的类别，从而将角度回归预测转换为分类任务，来消除角度边界不连续导致的损失。采用高斯窗口函数来平滑角度标签，并反映相邻角度类别的相关性。

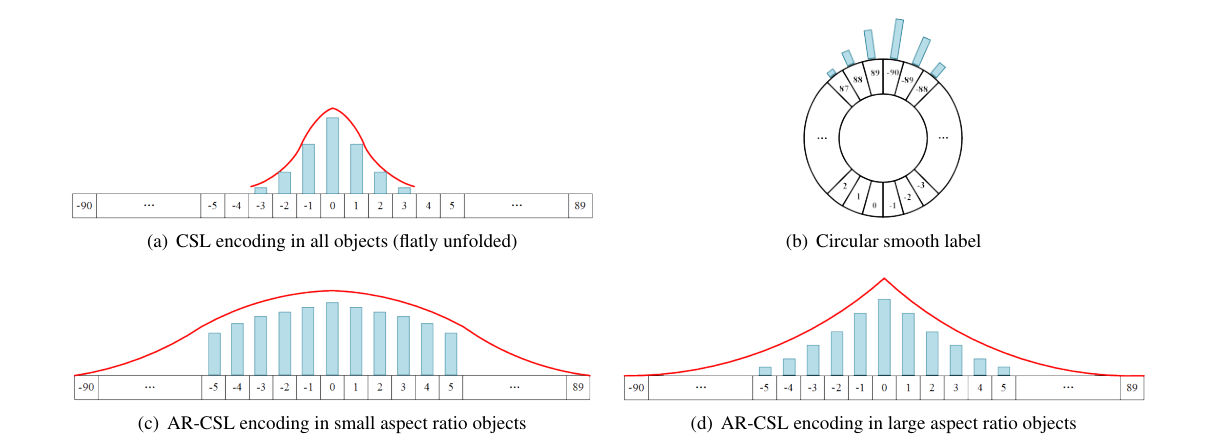
CSL的两个缺点：

• 固定的标签函数：高斯窗口函数
• 引入了超参数：窗口函数的半径，会极大的影响检测器的性能

AR-CSL：

$\operatorname{AR-CSL}(k, \Delta \theta)=\frac{\operatorname{SkewIoU}(k, \Delta \theta)-\operatorname{SkewIoU}(k)_{\min }}{1-\operatorname{SkewIoU}(k)_{\min }}$

$\begin{aligned} \operatorname{SkewIoU}(k, \Delta \theta) & =\left\{\begin{array}{rr} \frac{4 k \tan \Delta \theta-x-y}{4 k \tan \Delta \theta+x+y} & \Delta \theta \leq 2 \arctan \frac{1}{k} \\ \frac{4}{8 k \sin \Delta \theta-4} & \Delta \theta>2 \arctan \frac{1}{k} \end{array}\right. \\ x & =\left(1-k \tan \frac{\Delta \theta}{2}\right)^2 \tan ^2 \Delta \theta \\ y & =\left(\frac{-2 \sin ^2 \frac{\Delta \theta}{2}+k \sin \Delta \theta}{\cos \Delta \theta}\right)^2 \end{aligned}$

其中$k$是GT的横纵比。

这样让CSL的窗口函数，直接根据GT的横纵比变化，就可以弥补掉CSL的缺点。

Rotated Deformable Attention Module

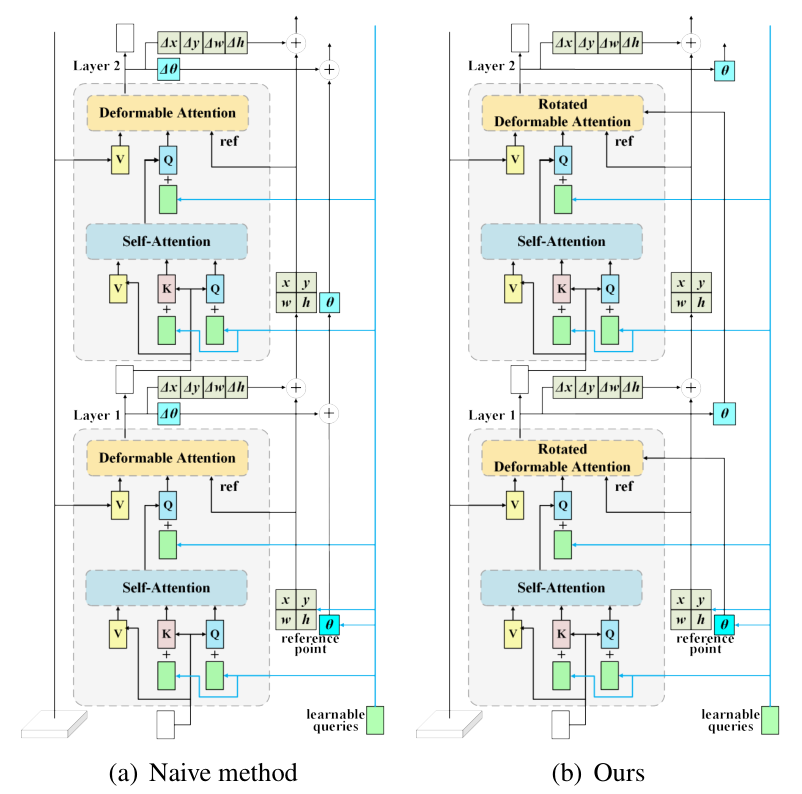
主要区别在这张图上很能反映出来了：

（a）：角度信息在每一层之后都是迭代更新的

（b）：把角度嵌入到Deformable Attention模块中，然后根据嵌入的角度信息旋转采样点，在每一层之后替换原来的角度。

Aspect Ratio Sensitive Weighting

$L_\theta \rightarrow \frac{k}{k+1} L_\theta, \quad C_\theta \rightarrow \frac{k}{k+1} C_\theta$

$k$ is the aspect ratio of the objects

Result

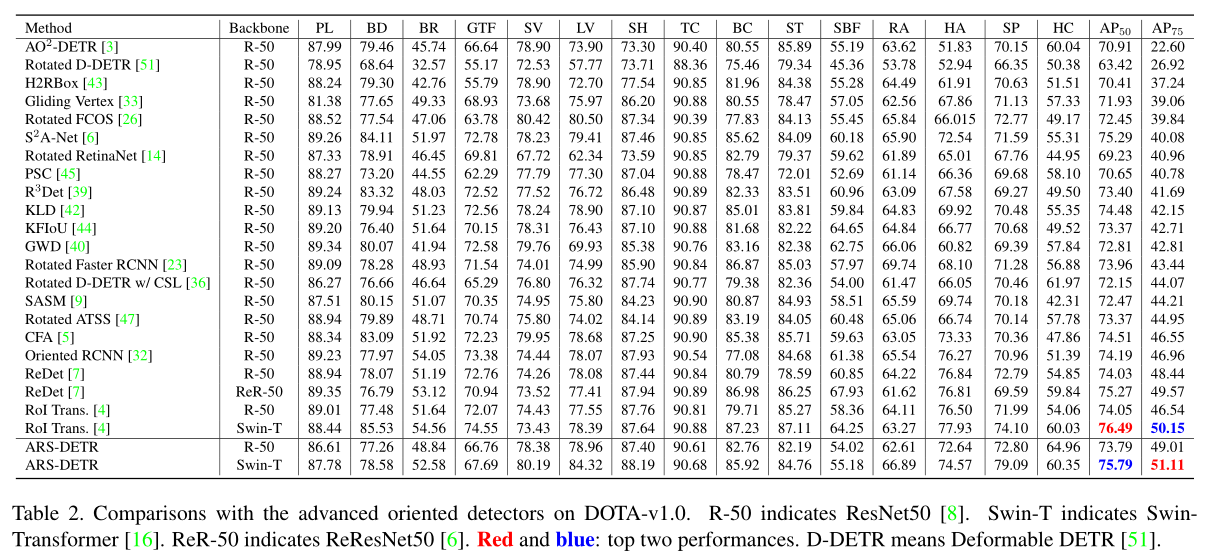
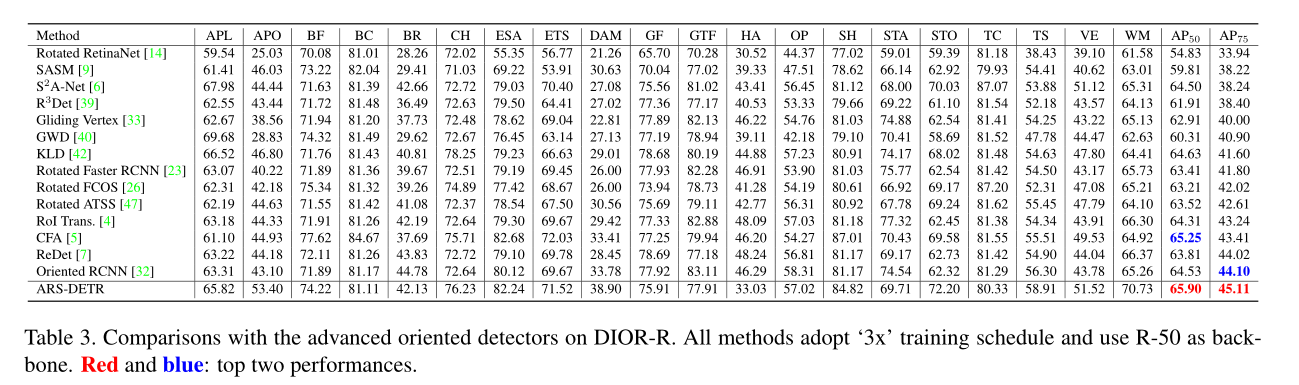
消融实验：