Phase-Shifting Coder
Phase-Shifting Coder
Introduction
论文题目 :Phase-Shifting Coder: Predicting Accurate Orientation in Oriented Object Detection
论文地址 :https://arxiv.org/pdf/2211.06368.pdf
论文出处 :2023’CVPR
代码实现 :https://github.com/open-mmlab/mmrotate/tree/1.x/configs/psc
Idea
这篇CVPR2023核心讨论是Boundary Problem
作者认为,产生边界问题的根本原因是:试图用连续函数拟合非连续函数
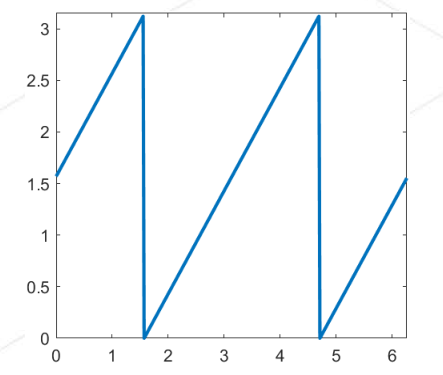
横坐标是输入图像的旋转角度,纵坐标是我们期望的输出角度
Detail
Review Boundary Problem
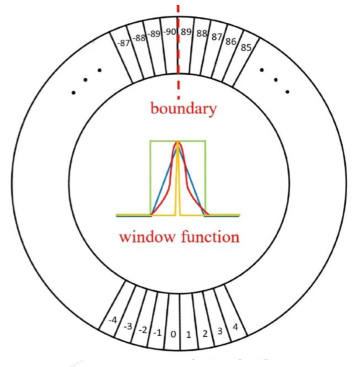
CSL 角度分类,固定的输出若干种角度。
缺点:没有办法输出连续的量,无法表示连续的整个角度周期。
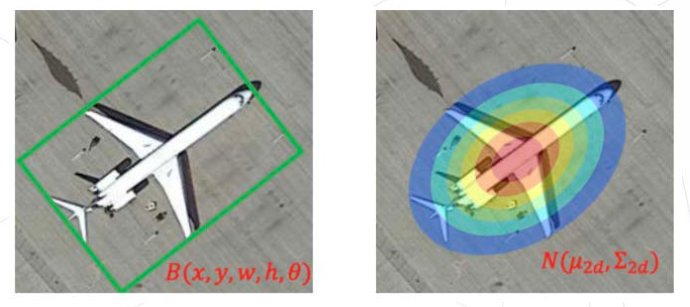
GWD 把旋转矩形框转化为二维高斯分布来计算Loss。
缺点:如果是方形目标的话,转换成高斯分布其实是没有角度的。
Consistent to inconsistent
作者认为,产生边界问题的根本原因是:试图用连续函数拟合非连续函数
作者是如何设计实验,来验证他的观点的呢?
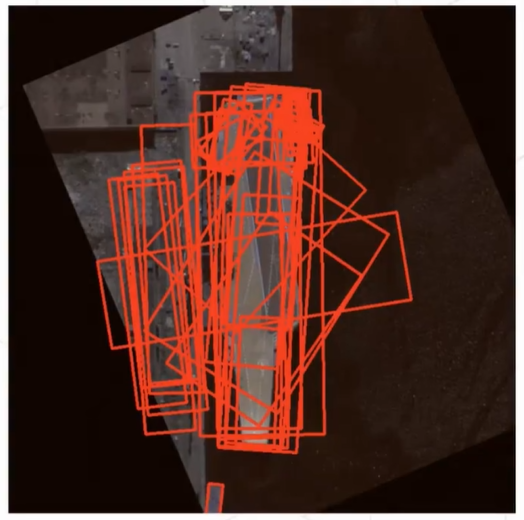
我们知道检测一张图片,实际上就是在这张图片的mutil-level frature map上划分多个grid(检测点),在每个点上预设anchor,然后在一定的检测范围内预测(不同level上的anchor scale不同,因此检测范围不同)。

如上图所示,作者在HSRC数据集上,找到一张GT的中心点正好在图片正中心的位置,靠近中心范围的白点(grid)都会对这艘船进行一个预测,最终得到了一系列的结果又会经过NMS,来得到一个最有可能的结果。
针对这张图片,作者设计实验验证:
- 选用一个连续网络, RetinaNet + GWD
- 将这张GT中心点正好在图片正中心的图片,围绕中心旋转
- 为排除NMS的不连续性影响,不使用NMS,只取正中心的检测点,观察其输出的检测框

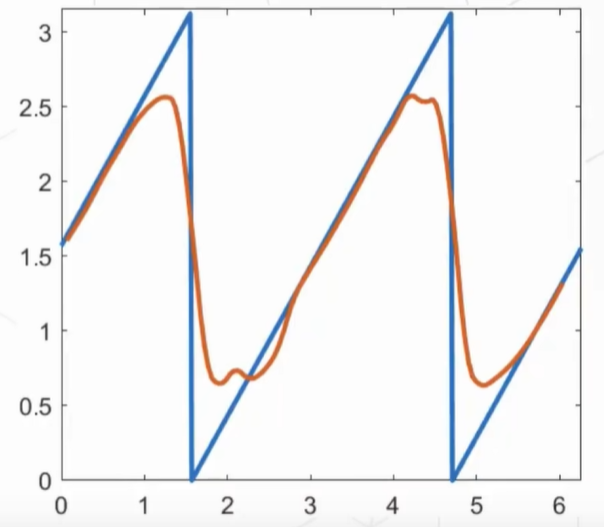
从右图中可以看到,在旋转的过程中,角度会有逐渐上升的过程,但是到了最顶上必须要有一个下降的过程而不能突然跳到最底部。就算网络训练的很好,这个下降过程非常快,也无法瞬间达到,因为连续性总归是有下降过程。
那么在这个下降过程就一定能找到一个输入图像,使得网络输出的预测角度是错的,(结合左图,每当到达边界值,都不是一瞬间)
GWD周围的点的到达边界值的周期各不相同,因此实际输出时,中心点的预测被NMS抑制了
因此,由卷积构成的连续函数模型不可能能直接学习出一个非连续函数模型。
Phase-Shifting Coder
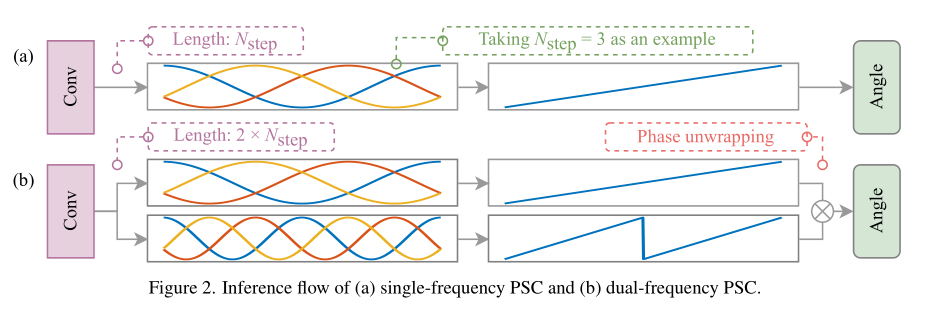
PSC的网络结构:
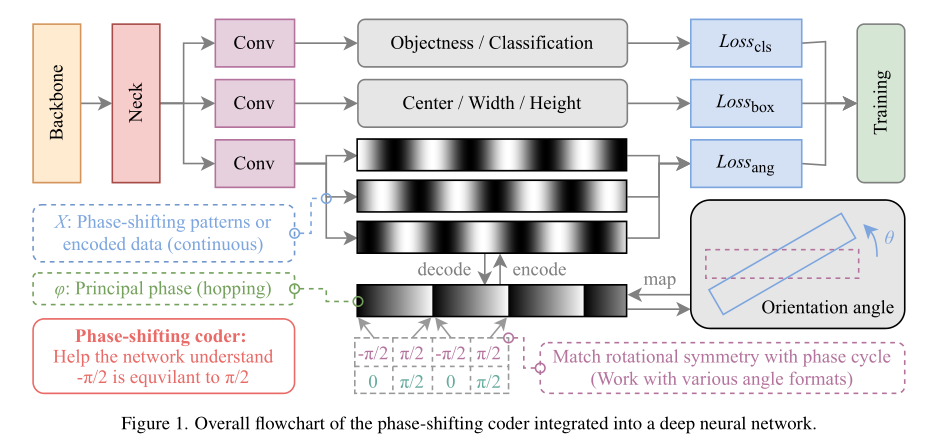
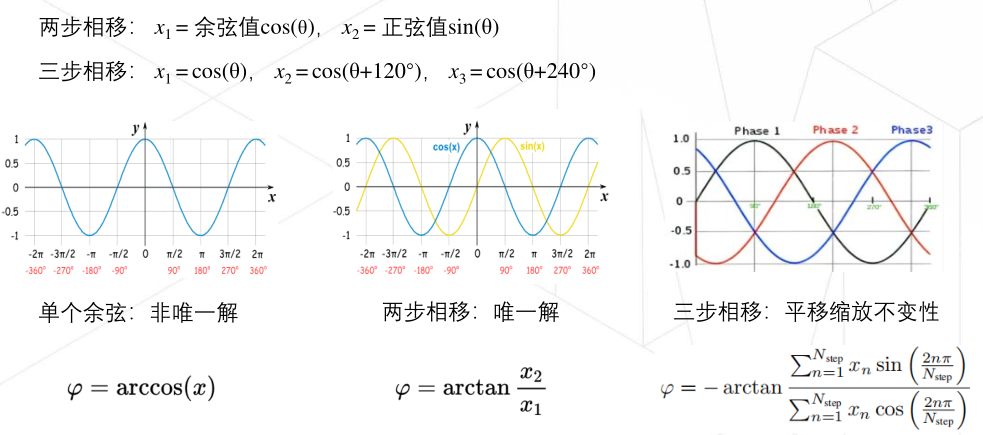
为什么是叫相移编码,也是来源于物理中光学,波长、相移、频率、周期等概念。
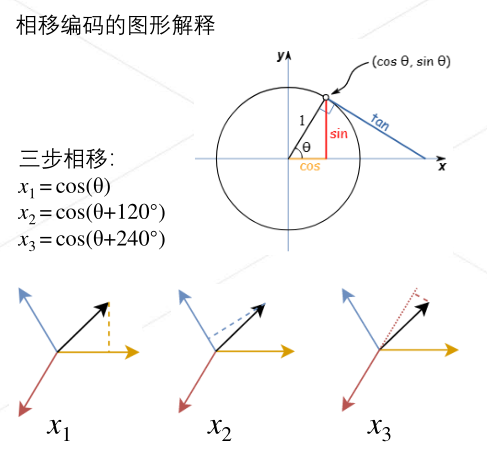
为什么PSC能够解决上述问题,学习出一个非连续函数模型?
用连续函数来预测连续变化的相位编码,然后在DeCode中使用arctan2将这个连续函数映射成非连续的角度。
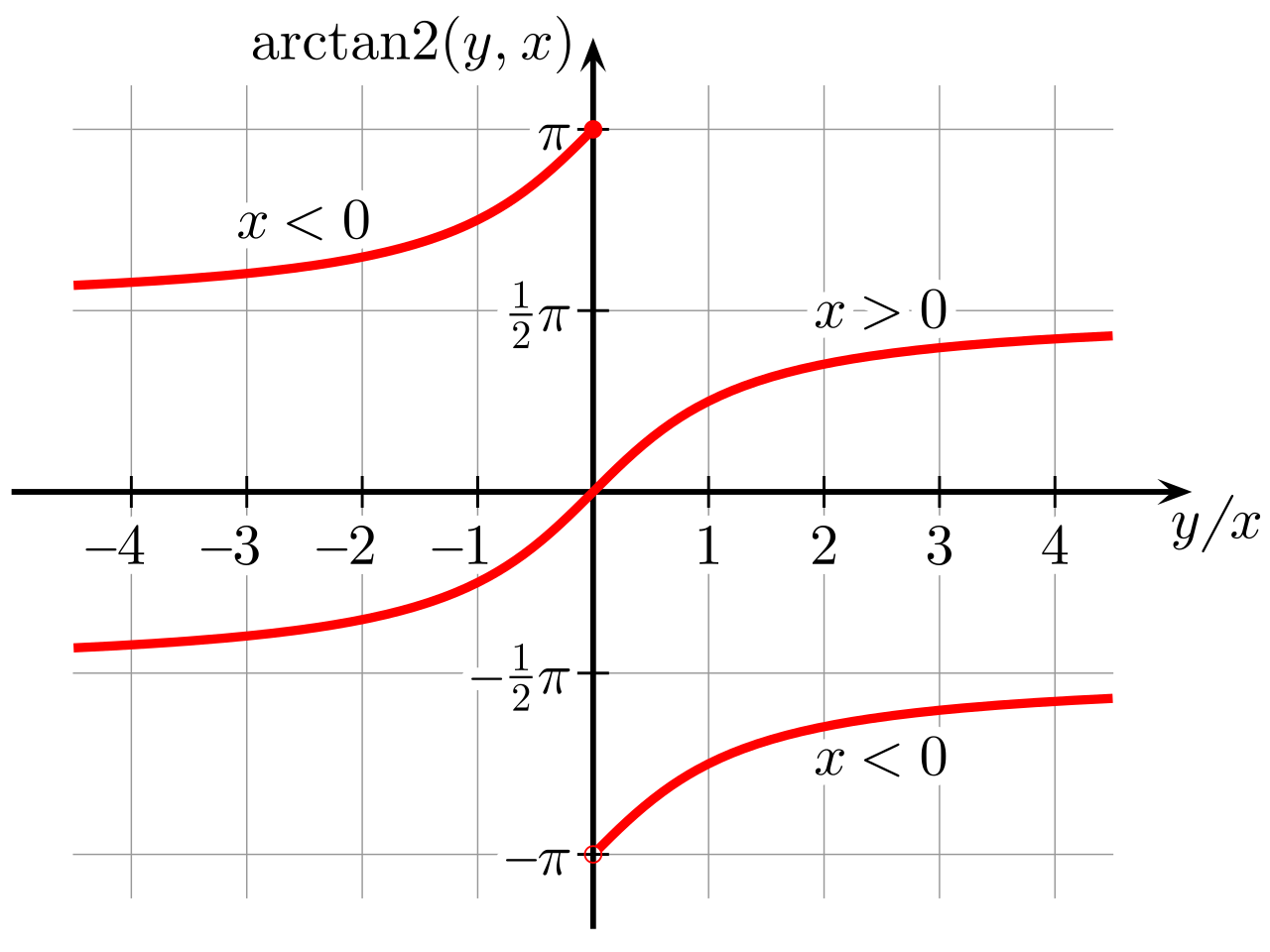
Phase-Shifting Coder Dual
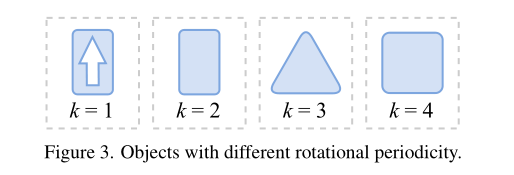
双频相移编码器,主要用于统一长方体和类正方体的角度周期不同的问题:

Result
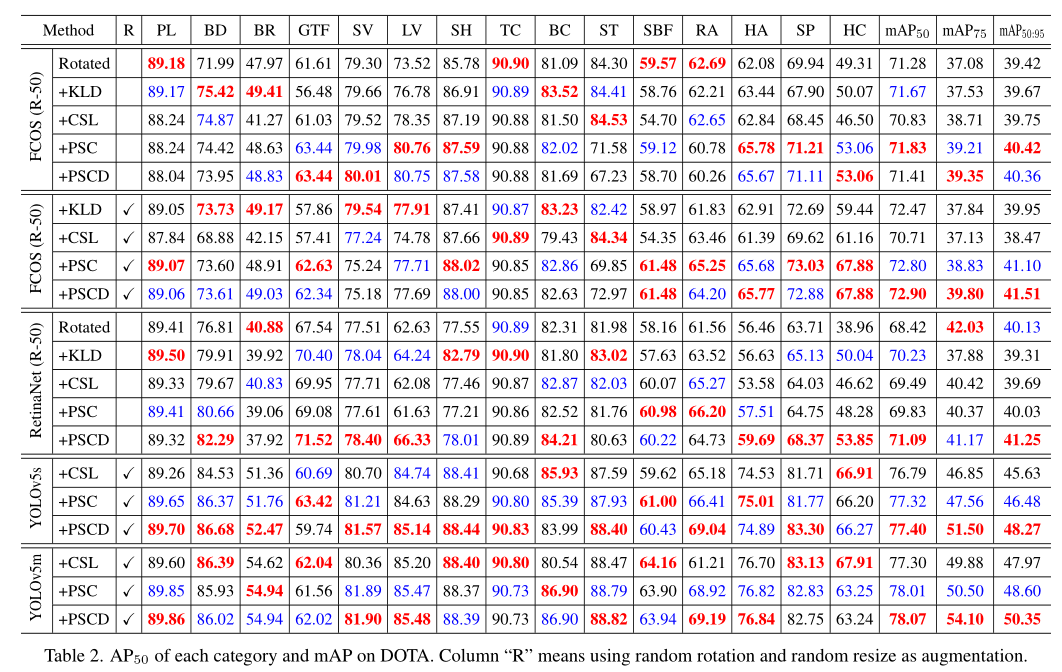
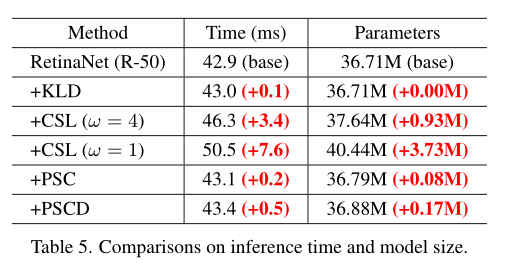
修改表达方式能否有这个问题?
本博客所有文章均采用 CC BY-NC-SA 4.0 协议 ,禁止商用,转载请注明出处!