Unleashing the Potential of Knowledge Distillation in Object Detection
Teaching with Uncertainty: Unleashing the Potential of Knowledge Distillation in Object Detection
Introduction
论文题目 :使用不确定性进行教学:释放目标检测知识蒸馏的潜力
论文地址 :https://arxiv.org/pdf/2406.06999v1.pdf
论文出处 :arXiv
代码实现:-
Idea
对于教师检测器来说,其获取的知识本身并不一定可靠,这是因为教师检测器的知识是通过训练优化参数学习而获得的。因此学生模型可能会被教师的不可靠知识所误导。因此作者提出了一种具有知识不确定性的基于特征蒸馏的检测范式。具体来说,作者使用了Mnote Carlo Dropout(MC Dropout)来估计教师模型的不确定知识,然后再将这些知识纳入学生模型。这种策略减轻了由于教师模型过度自信造成误导学生模型的风险,从而提高了学生模型的整体训练效果。
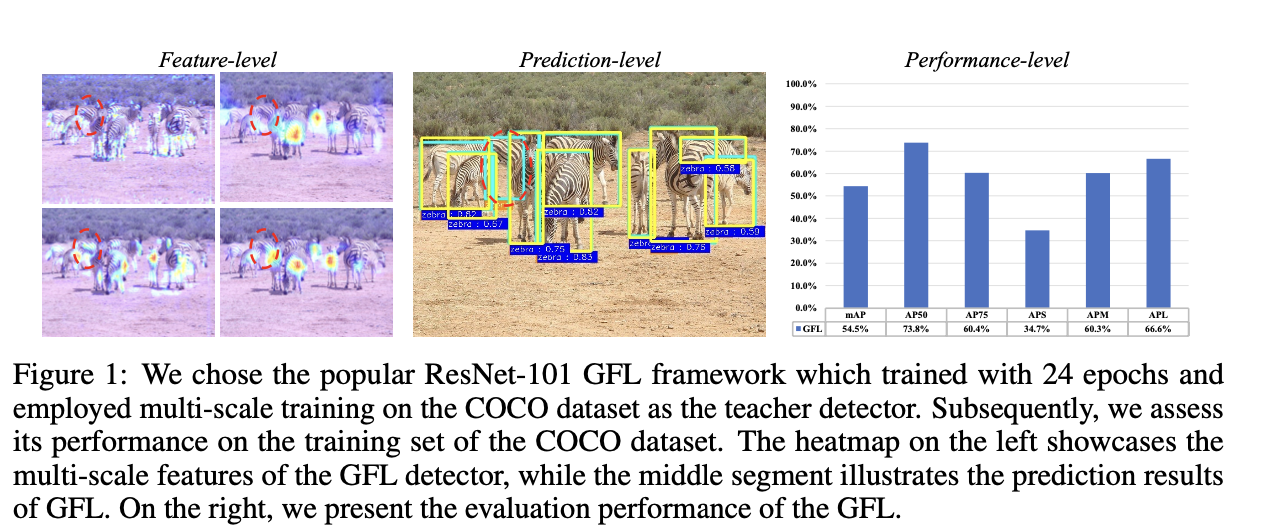
Detail
UET特征蒸馏检测架构如下:

MC Dropout采样次数默认为5次。Dropout ratio 起始是0.15,然后间隔0.05增长。
常规的特征蒸馏检测范式:
UET特征蒸馏检测范式:
其中.
在设计过程中保持了残差结构来避免不确定性与原本知识差距过大。
MC Dropout
对于一个模型的输出结果,我们想得到这个结果的方差来计算模型不确定性(认知不确定性)。而模型的参数是固定的,一个单独输出值是得不到方差的。如果说——我们能够用同一个模型,对同一个样本进行T次预测,而且这T次的预测值各不相同,就能够计算方差。
- 问题是同一个模型同一个样本,怎么得到不同的输出呢?
我们可以让学到的模型参数不是确定的值,而是服从一个分布,那么模型参数就可以从这个分布中采样得到,每一次采样,得到的模型参数都是不同的,这样模型产生的结果也是不同的,我们的目的就达到了。
- 但是如何让模型的参数不是确定的而是服从一个分布呢?
现成的 dropout 指的是在训练模型时使用 dropout 技术,使模型参数服从伯努利分布(例如,当 dropout 比例为 0.5 时,神经元中有一半会被 dropout)。在测试模型时估计不确定度,只需在预测时保持 dropout 开启,对同一输入进行 T 次预测,取平均值作为最终预测值,并计算方差来获取深度学习的不确定性。这种方法称为 MC Dropout 贝叶斯神经网络。MC Dropout 通过对同一输入进行多次前向传播,在 dropout 作用下产生不同网络结构的输出,将这些输出进行平均和统计方差,即可得到模型的预测结果及不确定度。这个过程可以并行,因此时间上相当于一次前向传播。
Result
在MC-COCO数据集上做测试:
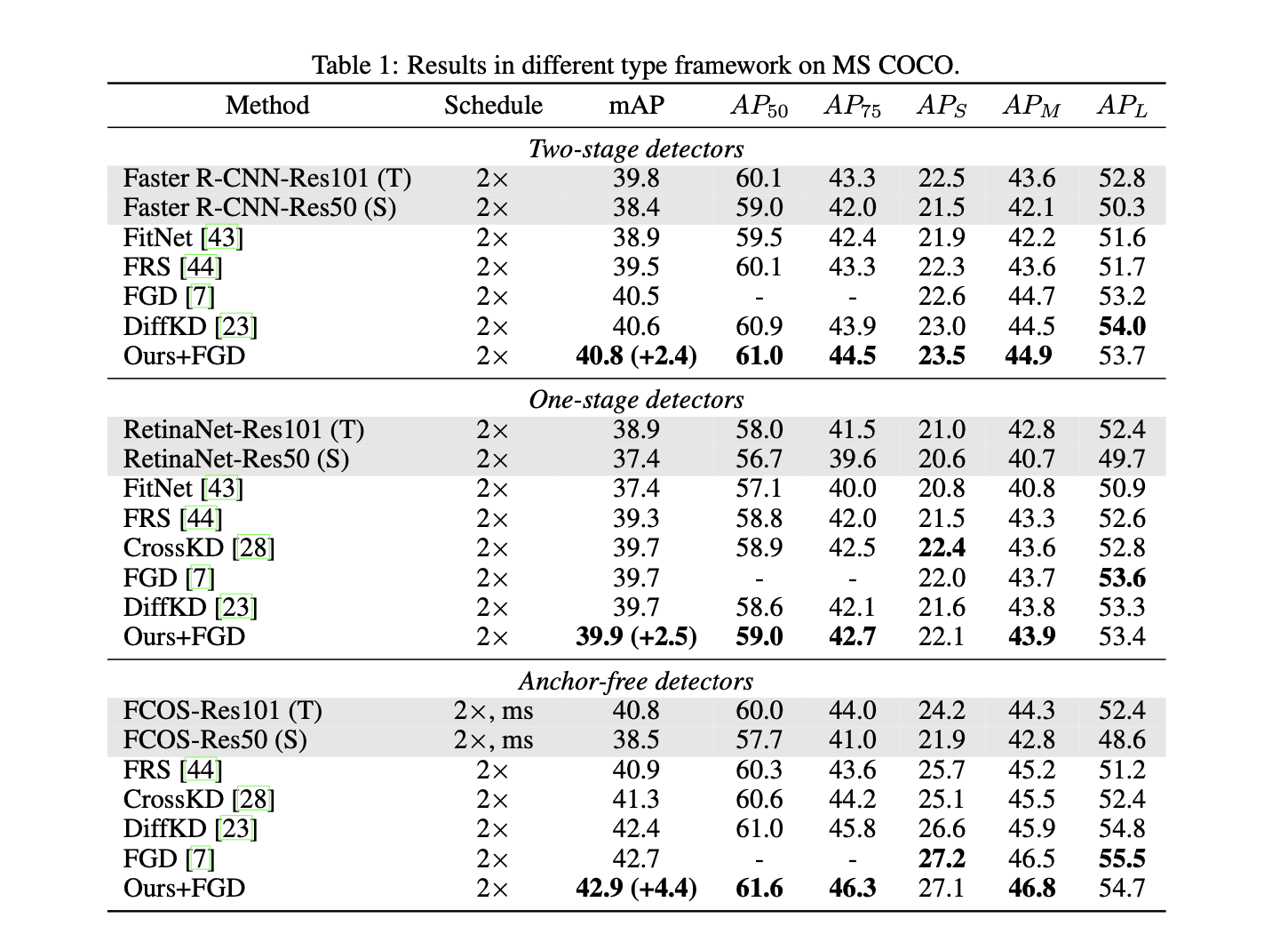
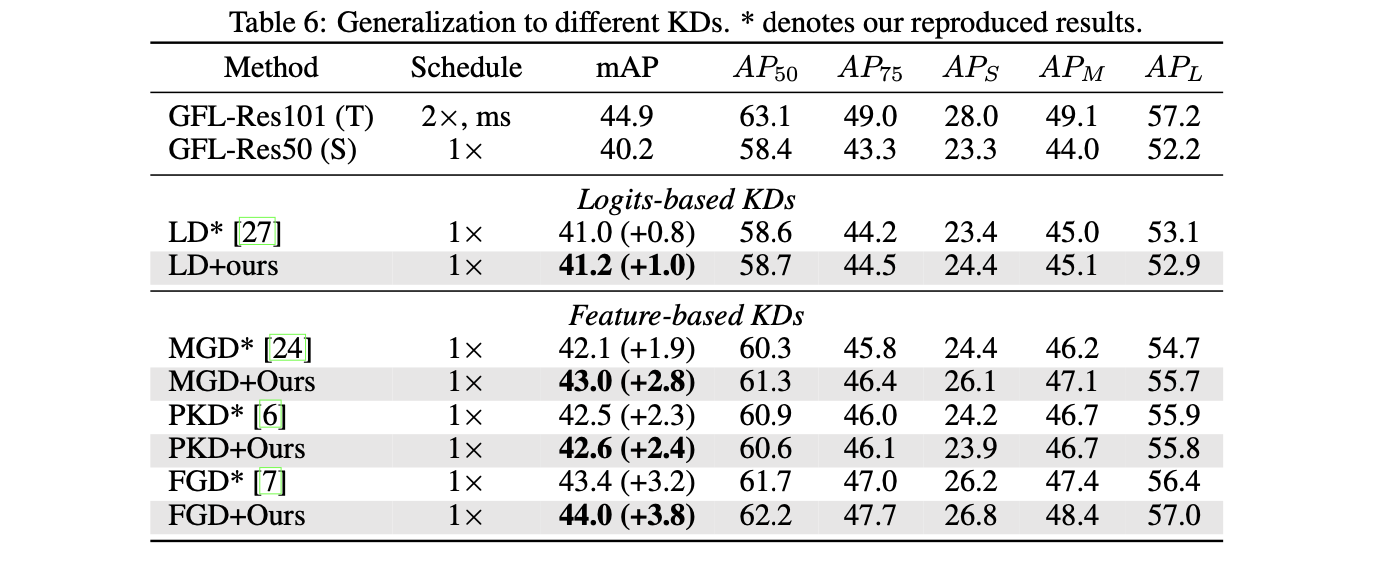
本博客所有文章均采用 CC BY-NC-SA 4.0 协议 ,禁止商用,转载请注明出处!